题目内容
17．若一次函数y=（m-1）x+3（m为常数）的图象经过第一、二、四象限，则m的取值范围是m＜1．分析 根据一次函数图象与系数的关系得到m-1＜0，然后求出不等式的解集即可．
解答 解：∵一次函数y=（m-1）x+3的图象经过第一、二、四象限，
∴m-1＜0，
解得m＜1．
故答案为：m＜1．
点评 本题考查的是一次函数的图象与系数的关系，即一次函数y=kx+b（k≠0）中，当k＜0，b＞0时函数的图象在一、二、四象限．
练习册系列答案
小学学习好帮手系列答案
小学同步三练核心密卷系列答案
相关题目
8．
如图，在以O为原点的直角坐标系中，矩形OABC的两边OC、OA分别在x轴、y轴的正半轴上，反比例函数y=$\frac{k}{x}$（x＞0）与AB相交于点D，与BC相交于点E，若BD=3AD，且△ODE的面积是9，则k=（ ）
如图，在以O为原点的直角坐标系中，矩形OABC的两边OC、OA分别在x轴、y轴的正半轴上，反比例函数y=$\frac{k}{x}$（x＞0）与AB相交于点D，与BC相交于点E，若BD=3AD，且△ODE的面积是9，则k=（ ）| A． | $\frac{9}{2}$ | B． | $\frac{27}{4}$ | C． | $\frac{24}{5}$ | D． | 12 |
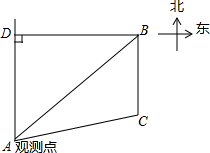已知B村庄位于A观测点北偏东53.2°方向，且其到A观测点正北方向的距离BD的长为24km，一辆摩托车从B村庄以60km/h的速度沿如图所示的BC方向航行，15min后达到C处，现测得C处位于A观测点北偏东79.8°方向，求此摩托车与A观测点之间的距离AC的长（精确到0.1km）．（参考数据：sin53.2°≈0.80，cos53.2°≈0.60，sin79.8°≈0.98，cos79.8°≈0.18，tan26.6°≈0.50，$\sqrt{2}$≈1.41，$\sqrt{5}$≈2.24．
12．-$\frac{1}{5}$的绝对值是（ ）
| A． | 5 | B． | -5 | C． | $\frac{1}{5}$ | D． | -$\frac{1}{5}$ |
2．
某校八年级全体男同学参加了跳绳比赛，从中随机抽取某班男同学的跳绳成绩，制作了如下频数分布表：
根据上面统计信息，解答下列问题：
（1）不全频数分布直方图．
（2）班级准备对跳绳成绩优秀的男同学进行奖励，奖励人数占班级男同学的20%，该班张辉同学的成绩为140个，通过计算判断张辉能否获得奖励．
（3）八年级共有200名男同学，若规定男同学的跳绳成绩在120个以上（含120个）为合格，估计该校八年级男同学成绩合格的人数．
某校八年级全体男同学参加了跳绳比赛，从中随机抽取某班男同学的跳绳成绩，制作了如下频数分布表：| 组别 | 99.5-109.5 | 109.5-119.5 | 119.5-129.5 | 129.5-139.5 | 139.5-149.5 | 149.5-159.5 |
| 频数 | 2 | 4 | 8 | 7 | 3 | 1 |
（1）不全频数分布直方图．
（2）班级准备对跳绳成绩优秀的男同学进行奖励，奖励人数占班级男同学的20%，该班张辉同学的成绩为140个，通过计算判断张辉能否获得奖励．
（3）八年级共有200名男同学，若规定男同学的跳绳成绩在120个以上（含120个）为合格，估计该校八年级男同学成绩合格的人数．
9．（$\frac{1}{2}$）2的相反数是（ ）
| A． | 4 | B． | -$\frac{1}{4}$ | C． | $\frac{1}{4}$ | D． | -4 |