题目内容
19.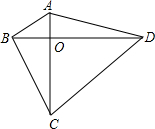 如图,四边形ABCD的对角线ACBD相交于点O,已知:OA=1,OB=2,OC=3,OD=4,CD=5.试求:
如图,四边形ABCD的对角线ACBD相交于点O,已知:OA=1,OB=2,OC=3,OD=4,CD=5.试求:(1)四边形ABCD的周长;
(2)四边形ABCD的面积.
分析 (1)根据OC=3,OD=4,CD=5,判断出△DCO为直角三角形且∠COD=90°,再根据勾股定理求出AD、AB、BC的长;
(2)根据四边形ABCD的面积为对角线长乘积的一半解答.
解答 解:(1)∵OC=3,OD=4,CD=5,
∴△DCO为直角三角形且∠COD=90°,
在Rt△DAO中,AD=$\sqrt{{1}^{2}+{4}^{2}}$=$\sqrt{17}$,
在Rt△BAO中,AB=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,
在Rt△BCO中,BC=$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$,
四边形ABCD的周长=$\sqrt{17}$+$\sqrt{5}$+$\sqrt{13}$+5.
(2)四边形ABCD的面积=$\frac{1}{2}$×(1+3)×(2+4)=12.
点评 本题考查了勾股定理、勾股定理的逆定理等知识,先判断出△DCO为直角三角形是解题的关键.

练习册系列答案
相关题目
14.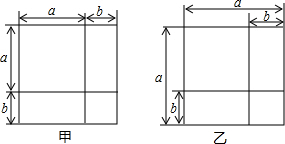 利用图形中面积的等量关系可以得到某些数学公式,例如,根据图甲,我们可以得到两数和的平方公式:(a+b)2=a2+2ab+b2.你根据图乙能得到的数学公式是( )
利用图形中面积的等量关系可以得到某些数学公式,例如,根据图甲,我们可以得到两数和的平方公式:(a+b)2=a2+2ab+b2.你根据图乙能得到的数学公式是( )
 利用图形中面积的等量关系可以得到某些数学公式,例如,根据图甲,我们可以得到两数和的平方公式:(a+b)2=a2+2ab+b2.你根据图乙能得到的数学公式是( )
利用图形中面积的等量关系可以得到某些数学公式,例如,根据图甲,我们可以得到两数和的平方公式:(a+b)2=a2+2ab+b2.你根据图乙能得到的数学公式是( )| A. | a2-b2=(a-b)2 | B. | (a+b)2=a2+2ab+b2 | C. | (a-b)2=a2-2ab+b2 | D. | a2-b2=(a+b)(a-b) |
11.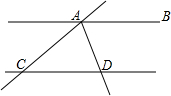 如图,AB∥CD,AD平分∠BAC,若∠ADC=70°,则∠ACD的度数为( )
如图,AB∥CD,AD平分∠BAC,若∠ADC=70°,则∠ACD的度数为( )
 如图,AB∥CD,AD平分∠BAC,若∠ADC=70°,则∠ACD的度数为( )
如图,AB∥CD,AD平分∠BAC,若∠ADC=70°,则∠ACD的度数为( )| A. | 35° | B. | 40° | C. | 45° | D. | 50° |
8. 如图,在以O为原点的直角坐标系中,矩形OABC的两边OC、OA分别在x轴、y轴的正半轴上,反比例函数y=$\frac{k}{x}$(x>0)与AB相交于点D,与BC相交于点E,若BD=3AD,且△ODE的面积是9,则k=( )
如图,在以O为原点的直角坐标系中,矩形OABC的两边OC、OA分别在x轴、y轴的正半轴上,反比例函数y=$\frac{k}{x}$(x>0)与AB相交于点D,与BC相交于点E,若BD=3AD,且△ODE的面积是9,则k=( )
 如图,在以O为原点的直角坐标系中,矩形OABC的两边OC、OA分别在x轴、y轴的正半轴上,反比例函数y=$\frac{k}{x}$(x>0)与AB相交于点D,与BC相交于点E,若BD=3AD,且△ODE的面积是9,则k=( )
如图,在以O为原点的直角坐标系中,矩形OABC的两边OC、OA分别在x轴、y轴的正半轴上,反比例函数y=$\frac{k}{x}$(x>0)与AB相交于点D,与BC相交于点E,若BD=3AD,且△ODE的面积是9,则k=( )| A. | $\frac{9}{2}$ | B. | $\frac{27}{4}$ | C. | $\frac{24}{5}$ | D. | 12 |
9.($\frac{1}{2}$)2的相反数是( )
| A. | 4 | B. | -$\frac{1}{4}$ | C. | $\frac{1}{4}$ | D. | -4 |
 如图,在长和宽分别是11和10的矩形内,放置了如图中5个大小相同的正方形,则正方形的边长是$\sqrt{10}$.
如图,在长和宽分别是11和10的矩形内,放置了如图中5个大小相同的正方形,则正方形的边长是$\sqrt{10}$.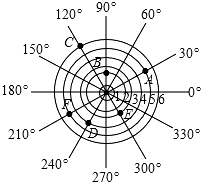 如图,雷达探测器测得六个目标A、B、C、D、E、F出现,按照规定的目标表示方法,目标A、E的位置表示为A(5,30°),E(3,300°),则目标C的位置表示为(6,120°).
如图,雷达探测器测得六个目标A、B、C、D、E、F出现,按照规定的目标表示方法,目标A、E的位置表示为A(5,30°),E(3,300°),则目标C的位置表示为(6,120°).