题目内容
2.将抛物线y=-3x2经过怎样的平移使它经过点O(0,0)和点A(1,9)?写出平移后抛物线的解析式.分析 先利用待定系数法求平移后的抛物线解析式,得到平移后抛物线的顶点坐标,然后利用顶点的平移规律可得到抛物线平移的情况.
解答 解:设平移后的抛物线解析式为y=-3(x-m)2+n,
把O(0,0)和点A(1,9)代入得$\left\{\begin{array}{l}{-3{m}^{2}+n=0}\\{-3(1-m)^{2}+n=9}\end{array}\right.$,解得$\left\{\begin{array}{l}{m=2}\\{n=12}\end{array}\right.$,
所以平移后的抛物线解析式为y=-3(x-2)2+12,抛物线的顶点坐标为(2,12),
而抛物线y=-3x2的顶点坐标为(0,0),
因为点(0,0)向右平移2个单位,再向上平移12个单位得到点(2,12),
所以将抛物线y=-3x2向右平移2个单位,再向上平移12个单位使它经过点O(0,0)和点A(1,9).
点评 本题考查了二次函数图象与几何变换:由于抛物线平移后的形状不变,故a不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.

练习册系列答案
相关题目
7.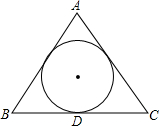 如图所示.在等边△ABC中,△ABC的内切圆半径是3,则△ABC的周长为( )
如图所示.在等边△ABC中,△ABC的内切圆半径是3,则△ABC的周长为( )
 如图所示.在等边△ABC中,△ABC的内切圆半径是3,则△ABC的周长为( )
如图所示.在等边△ABC中,△ABC的内切圆半径是3,则△ABC的周长为( )| A. | 9$\sqrt{3}$ | B. | 18 | C. | 18$\sqrt{3}$ | D. | 54 |
 )
) 
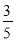 B.
B. 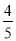 C.
C. 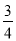 D.
D. 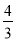
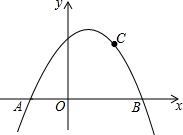 如图,抛物线y=ax2+bx+c关于直线x=1对称,与坐标轴交于A,B两点,且AB=4,点C(2,$\frac{3}{2}$)在抛物线上.求抛物线的解析式.
如图,抛物线y=ax2+bx+c关于直线x=1对称,与坐标轴交于A,B两点,且AB=4,点C(2,$\frac{3}{2}$)在抛物线上.求抛物线的解析式.