题目内容
17.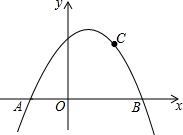 如图,抛物线y=ax2+bx+c关于直线x=1对称,与坐标轴交于A,B两点,且AB=4,点C(2,$\frac{3}{2}$)在抛物线上.求抛物线的解析式.
如图,抛物线y=ax2+bx+c关于直线x=1对称,与坐标轴交于A,B两点,且AB=4,点C(2,$\frac{3}{2}$)在抛物线上.求抛物线的解析式.
分析 首先根据对称轴以及A和B是对称点求得A和B的坐标,然后利用待定系数法求得函数的解析式.
解答 解:抛物线的对称轴是x=1,AB=4,则A的坐标是(-1,0),B的坐标是(3,0).
根据题意得:$\left\{\begin{array}{l}{a-b+c=0}\\{9a+3b+c=0}\\{4a+2b+c=\frac{3}{2}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{b=1}\\{c=\frac{3}{2}}\end{array}\right.$.
则抛物线的解析式是y=-$\frac{1}{2}$x2+x+$\frac{3}{2}$.
点评 本题考查了待定系数法求函数的解析式,根据对称性求得A和B的坐标是解决本题的关键.

练习册系列答案
相关题目
 B.
B.  C.
C.  D.
D. 
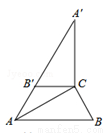
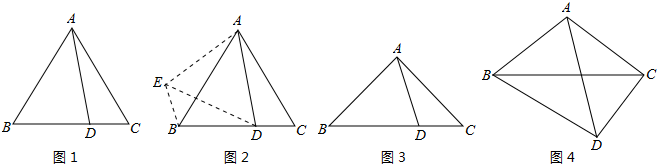
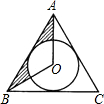 如图,已知等边三角形ABC的边长是6,⊙O是它的内切圆,则图中阴影部分的面积是3$\sqrt{3}$-π.
如图,已知等边三角形ABC的边长是6,⊙O是它的内切圆,则图中阴影部分的面积是3$\sqrt{3}$-π.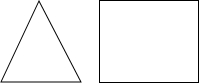 一个几何体的主视图和左视图如图所示,它是什么几何体?请补画这个几何体的俯视图.
一个几何体的主视图和左视图如图所示,它是什么几何体?请补画这个几何体的俯视图.