题目内容
2.解下列不等式(组),并把它们的解集在数轴上表示出来:(1)-2m+6>3m-24

(2)$\left\{\begin{array}{l}{3(x+2)>x+8}\\{\frac{x}{4}≥\frac{x-1}{3}}\end{array}\right.$

分析 (1)首先移项,再合并同类项,最后把x的系数化为1即可;
(2)首先分别解出两个不等式的解集,再根据解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到确定不等式组的解集.
解答 解:(1)-2m+6>3m-24,
-2m-3m>-24-6,
-5m>-30,
m<6,
在数轴上表示: ;
;
(2)$\left\{\begin{array}{l}{3(x+2)>x+8①}\\{\frac{x}{4}≥\frac{x-1}{3}②}\end{array}\right.$,
由①得:x>1,
由②得:x≤4,
不等式组的解集为:1<x≤4,
在数轴上表示: .
.
点评 此题主要考查了解一元一次不等式(组),以及在数轴上表示不等式的解集,关键是掌握解一元一次不等式与解一元一次方程基本相同,掌握解集的规律.(>,≥向右画;<,≤向左画),在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
14.在“我为贫困留守儿童献爱心”捐款活动中,某校八年级(2)班50名同学捐款情况如下表:
在这次活动中,该班同学捐款金额的众数是( )
| 金额/元 | 20 | 30 | 35 | 50 | 100 |
| 学生/人 | 8 | 10 | 6 | 18 | 8 |
| A. | 50元 | B. | 100元 | C. | 35元 | D. | 30元 |
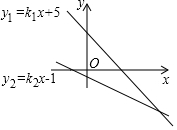 有两个一次函数:y1=k1x+5,y2=k2x-1.它们的图象交于点(5,-3),如图.那么,不等式(k1-k2)x<-6的解集是x>5.
有两个一次函数:y1=k1x+5,y2=k2x-1.它们的图象交于点(5,-3),如图.那么,不等式(k1-k2)x<-6的解集是x>5.