��Ŀ����
�����¶���һ�������Σ���һ���������д������ߵ�ƽ������ڵ������ϸߵ�ƽ����������������Ϊ���ɸ������Σ����߽���Ϊ���ɶ��㣮
��������֪
�ٵ���ֱ�������� ���ɸ������Σ�����д���ǡ����ߡ����ǡ�����
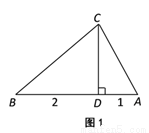
����ͼ1����֪��ABCΪ���ɸ������Σ�����CΪ���ɶ��㣬CD��AB���ϵĸߣ��� �������߶�CD�ij��ȣ�
�������߶�CD�ij��ȣ�
������̽��
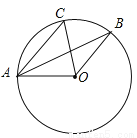
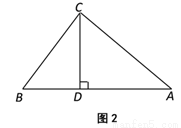
��ͼ2����֪��ABCΪ���ɸ������Σ�����CΪ���ɶ�����CA��CB��CD��AB���ϵĸߣ���̽���߶�AD��CB��������ϵ��������֤����
���ƹ�Ӧ��
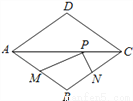
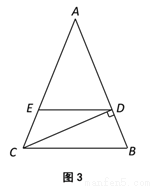
��ͼ3��������ABCΪ���ɸ������Σ�����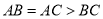 ��CDΪAB���ϵĸߣ�����D��BC����ƽ������AC�߽��ڵ�E����
��CDΪAB���ϵĸߣ�����D��BC����ƽ������AC�߽��ڵ�E����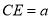 �������߶�DE�ij��ȣ�
�������߶�DE�ij��ȣ�
��ϰ��ϵ�д�
�����Ŀ


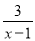 =1 B.
=1 B. 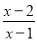 +x=
+x=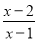 +1 C.
+1 C. 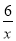 ��
��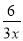 =2 D.
=2 D. 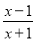 =
=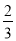
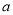 ������������Ӱ���ֵ����Ϊ�� ��
������������Ӱ���ֵ����Ϊ�� ��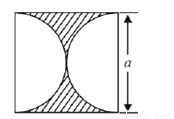
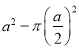 B.
B. 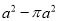 C.
C. 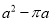 D.
D. 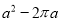
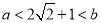 ��
��