题目内容
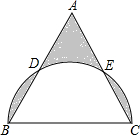 如图,在边长为2的正三角形ABC中,以BC为直径的半圆分别交AB、AC于点D、E.则图中阴影部分的面积是
如图,在边长为2的正三角形ABC中,以BC为直径的半圆分别交AB、AC于点D、E.则图中阴影部分的面积是考点:扇形面积的计算,等边三角形的性质
专题:
分析:如图,取BC的中点O,连接OD、OE、DE.利用三角形中位线定理和等边三角形的判定得到△OBD、△ODE、△OEC均为等边三角形.如图所示,阴影①、③和空白②的面积是相等的,先将阴影①移到空白②的位置,则△ADE的面积就等于④的面积,再将阴影③移到空白②的位置,则三个阴影部分的面积就等于扇形DOE的面积,也就是半圆的面积的
,利用圆的面积公式即可求解.
| 1 |
| 3 |
解答: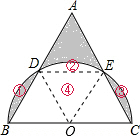 解:π×(2÷2)2×
解:π×(2÷2)2×
×
=
.
故答案是:
.
 解:π×(2÷2)2×
解:π×(2÷2)2×| 1 |
| 2 |
| 1 |
| 3 |
| π |
| 6 |
故答案是:
| π |
| 6 |
点评:本题考查了等边三角形的性质、扇形面积的计算.解答此题的关键是将阴影部分重新组合,得到阴影部分的面积等于半圆的面积的
,问题即可得解.
| 1 |
| 3 |

练习册系列答案
 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
计算(-2a3b)2的结果是( )
| A、-2a6b |
| B、4a6b2 |
| C、-4a6b2 |
| D、4a5b2 |
下列图案中,是中心对称又是轴对称的图形是( )
A、 |
B、 |
C、 |
D、 |
 如图,已知直线l⊥x轴于点D,点B(-1,y)为直线l上的动点,点C(x,0)为x轴上的动点,且-1<x<4,若点A(4,5),AC⊥BC,则y与x之间的函数关系式
如图,已知直线l⊥x轴于点D,点B(-1,y)为直线l上的动点,点C(x,0)为x轴上的动点,且-1<x<4,若点A(4,5),AC⊥BC,则y与x之间的函数关系式