如图.把一个图形先沿着一条直线进行轴对称变换.再沿着与这条直线平行的方向平移.我们把这样的图形变换叫做滑动对称变换.你认为在滑动对称变换过程中.对应点不在变换直线上的两个对应三角形的对应点所具有的性质是( )A．对应点连线与对称轴垂直B．对应点连线被对称轴平分C．对应点连线被对称轴垂直平分D．对应点连线互相平行题目和参考答案——青夏教育精英家教网—

题目内容

14．

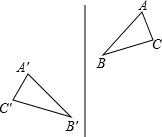如图，把一个图形先沿着一条直线进行轴对称变换，再沿着与这条直线平行的方向平移，我们把这样的图形变换叫做滑动对称变换，你认为在滑动对称变换过程中，对应点不在变换直线上的两个对应三角形的对应点所具有的性质是（　　）

	A．	对应点连线与对称轴垂直		B．	对应点连线被对称轴平分
	C．	对应点连线被对称轴垂直平分		D．	对应点连线互相平行

分析直接利用轴对称图形的性质得出对应点之间的关系．

解答解：两个对应三角形的对应点所具有的性质是对应点连线被对称轴平分．
故选：B．

点评此题主要考查了轴对称的性质，正确把握对应点之间关系是解题关键．

练习册系列答案

寒假作业西南师范大学出版社系列答案

桂壮红皮书寒假作业河北人民出版社系列答案

寒假课程练习南方出版社系列答案

一路领先寒假作业河北美术出版社系列答案

寒假作业美妙假期云南科技出版社系列答案

相关题目

3．下列四个几何图形中，俯视图是矩形的是（　　）

	A．	-3³a²bc²的系数为-3，次数为27		B．	$\frac{x}{π}$+$\frac{y}{2}$+$\frac{{z}^{2}}{3}$不是单项式，但是整式
	C．	$\frac{1}{x+1}$是多项式		D．	mx²+1一定是关于x的二次二项式

2．将一元二次方程4（x²+1）=5x化为一般形式是4x²-5x+4=0．

9．2015武汉园博园开幕，预计国庆期间共接待游客48万人，48万用科学记数法表示为4.8×10⁵．

19．平面内一点P离⊙O上的点最近距离为5cm，离⊙O上的点最远距离为13cm，则⊙O的半径为（　　）

6．若y=$\sqrt{x-2}$+$\sqrt{2-x}$-3，则P（x，y）在（　　）

3．

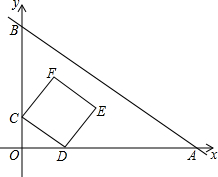如图，在平面直角坐标系中，直线AB经过点A（4，0），B（0，3），动点C从点O出发，以每秒3个单位长度的速度向点B运动，过点C作CD∥AB于OA于点D，以CD为边向上作正方形CDEF，设正方形CDEF与△AOB重合部分图形的面积为y，运动时间为t．
（1）用含t的式子表示E，F两点的坐标；
（2）求y与t的函数关系式；
（3）过点A，B分别作x铀、y轴的垂线，两垂线交于点H，当正方形的顶点落在AH或BH边上时，求t的值．
（4）在点D向点A运动的过程中，连接AE，BF，分别以CF，DE为对称轴，作△BCF和△ADE的轴对称三角形△B′CF，△A′DE，当1≤A′B′≤4时，直接写出t的取值范围．

4．

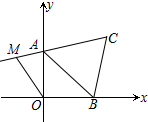如图所示，在平面直角坐标系中，A（0，3）、B（3，0）、C（4，4），线段CA的延长线上有一点M，使四边形ABOM的面积与三角形ABC的面积相等，则M的坐标为（-2，$\frac{5}{2}$）．

试题分类