题目内容
3.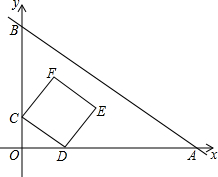 如图,在平面直角坐标系中,直线AB经过点A(4,0),B(0,3),动点C从点O出发,以每秒3个单位长度的速度向点B运动,过点C作CD∥AB于OA于点D,以CD为边向上作正方形CDEF,设正方形CDEF与△AOB重合部分图形的面积为y,运动时间为t.
如图,在平面直角坐标系中,直线AB经过点A(4,0),B(0,3),动点C从点O出发,以每秒3个单位长度的速度向点B运动,过点C作CD∥AB于OA于点D,以CD为边向上作正方形CDEF,设正方形CDEF与△AOB重合部分图形的面积为y,运动时间为t.(1)用含t的式子表示E,F两点的坐标;
(2)求y与t的函数关系式;
(3)过点A,B分别作x铀、y轴的垂线,两垂线交于点H,当正方形的顶点落在AH或BH边上时,求t的值.
(4)在点D向点A运动的过程中,连接AE,BF,分别以CF,DE为对称轴,作△BCF和△ADE的轴对称三角形△B′CF,△A′DE,当1≤A′B′≤4时,直接写出t的取值范围.
分析 (1)如图1中,作EM⊥OA于M,EN⊥OB于N,只要证明△CNF≌△DOC,△DOC≌△EMD,推出CN=OD=EM=4t,FN=OC=DM=3t,由此即可解决问题.
(2)分两种情形①当0<t≤$\frac{12}{37}$时,重叠部分就是正方形CDEF,如图1,②当$\frac{12}{37}$<t<1时,重叠部分是四边形CDGH,如图2中,分别求解即可.
(3)分三种情形①如图3中,当点F在BH上时,由△CBF≌△DOC可知BC=OD=4t,列方程求解.②如图4中,当点E在AH上时,由△ADE≌△OCD可得AD=OC=3t,
列方程求解.③当C、D在AH、BH上时,t=1.
(4)分两种情形讨论①当A′在B′上方时,如图5中,②当A′在B′下方时,如图6中,分别列出不等式组即可解决问题.
解答 解:(1)如图1中,作EM⊥OA于M,EN⊥OB于N.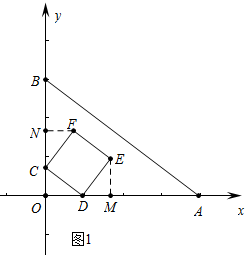
∵四边形ABCD是正方形,
∴CD=CF,∠FCD=90°,
∴∠FCN+∠DCO=90°,∠DCO+∠CDO=90°,
∴∠FCN=∠CDO,∵∠CNF=∠DOC=90°,
∴△CNF≌△DOC,同理可证△DOC≌△EMD,
∴CN=OD=EM,FN=OC=DM,
∵CD∥AB,
∴$\frac{OC}{OB}$=$\frac{OD}{OA}$,
∴$\frac{3t}{3}$=$\frac{OD}{4}$,
∴OD=4t,
∴CN=OD=EM=4t,FN=OC=DM=3t,
∴F(3t,7t),E(7t,4t).
(2)设直线AB的解析式为y=kx+b,则有$\left\{\begin{array}{l}{b=3}\\{4k+b=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-\frac{3}{4}}\\{b=3}\end{array}\right.$,
∴直线AB解析式为y=-$\frac{3}{4}$x+3,
当点E在AB上时,4t=-$\frac{3}{4}$×7t+3,解得t=$\frac{12}{37}$,
∴当0<t≤$\frac{12}{37}$时,重叠部分就是正方形CDEF,如图1,S=25t2.
当$\frac{12}{37}$<t<1时,重叠部分是四边形CDGH,如图2中,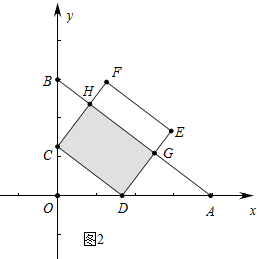
∵∠A=∠A,∠DGA=∠AOB,
∴△ADG∽△ABO,
∴$\frac{DG}{OB}$=$\frac{AD}{AB}$,
∴$\frac{DG}{3}$=$\frac{4-4t}{5}$,
∴DG=$\frac{3}{5}$(4-4t),
∴S=5t×$\frac{3}{5}$(4-4t)=-12t2=12t,
综上所述,S=$\left\{\begin{array}{l}{25{t}^{2}}&{(0<t≤\frac{12}{37})}\\{-12{t}^{2}+12t}&{(\frac{12}{37}<t<1)}\end{array}\right.$.
(3)如图3中,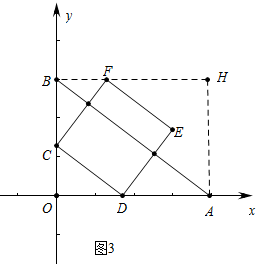
当点F在BH上时,由△CBF≌△DOC可知BC=OD=4t,
∴3t+4t=3,
∴t=$\frac{3}{7}$,时点F在BH上.
如图4中,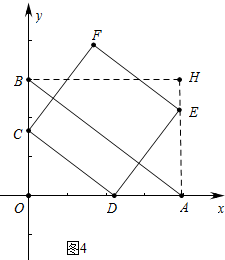
当点E在AH上时,由△ADE≌△OCD可得AD=OC=3t,
∴4t+3t=4,
∴t=$\frac{4}{7}$时,点E在AH上.
当C、D在AH、BH上时,t=1
综上所述,t=$\frac{3}{7}$或$\frac{4}{7}$或1秒时,正方形的顶点落在AH或BH边上.
(4)当A′在B′上方时,如图5中,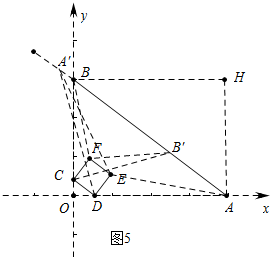
A′B′=AA′-5+BB′=$\frac{4}{5}$(4-4t)+$\frac{3}{5}$(3-3t)-5=5-10t,
由题意:1≤5-10t≤4,
解得$\frac{1}{10}$≤t≤$\frac{2}{5}$.
当A′在B′下方时,如图6中,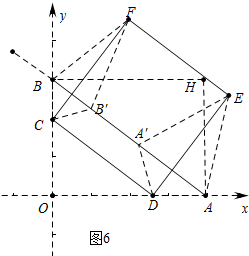
A′B′=5-AA′-BB′=10t-5,
由题意1≤10t-5≤4,
解得$\frac{3}{5}$≤t$≤\frac{9}{10}$,
综上所述,$\frac{1}{10}$≤t≤$\frac{2}{5}$或$\frac{3}{5}$≤t$≤\frac{9}{10}$时,1≤A′B′≤4.
点评 本题考查四边形综合题、正方形的性质、矩形的性质、全等三角形的判定和性质、翻折变换等知识,解题的关键是学会分类讨论,学会画好图象解决问题,学会把问题转化为方程或不等式组解决,属于中考压轴题.

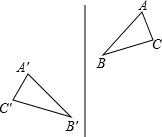 如图,把一个图形先沿着一条直线进行轴对称变换,再沿着与这条直线平行的方向平移,我们把这样的图形变换叫做滑动对称变换,你认为在滑动对称变换过程中,对应点不在变换直线上的两个对应三角形的对应点所具有的性质是( )
如图,把一个图形先沿着一条直线进行轴对称变换,再沿着与这条直线平行的方向平移,我们把这样的图形变换叫做滑动对称变换,你认为在滑动对称变换过程中,对应点不在变换直线上的两个对应三角形的对应点所具有的性质是( )| A. | 对应点连线与对称轴垂直 | B. | 对应点连线被对称轴平分 | ||
| C. | 对应点连线被对称轴垂直平分 | D. | 对应点连线互相平行 |
| A. | 0~1 | B. | 1~2 | C. | 2~3 | D. | 3~4 |
 如图所示,直线AB∥CD,∠BAE=28°,∠DCE=50°,则∠AEC=78°.
如图所示,直线AB∥CD,∠BAE=28°,∠DCE=50°,则∠AEC=78°.