题目内容
如图，已知D、E、F分别为等腰△ABC边BC、CA、AB上的点，如果AB=AC，∠FDE=∠B，BD=2，CD=3，CE=4，AE=1，那么AF的长为（ ）| A、3.5 | B、4 | C、4.5 | D、5 |
考点：相似三角形的判定与性质
专题：
分析：证明∠BFD=∠CDE、∠B=∠C，得到△BDF∽△CCED；进而得到BD：CE=BF：DC，求出BF的长度，即可解决问题．
解答：解：∵AB=AC，
∴∠B=∠C；
又∵∠FDE=∠B，
∴∠BFD+∠BDF=∠BDF+∠CDE，
∴∠BFD=∠CDE，而∠B=∠C，
∴△BDF∽△CCED，
∴BD：CE=BF：DC，
而BD=2，CD=3，CE=4，
∴BF=1.5，
∵AB=AC=1+4=5，
∴AF=5-1.5=3.5．
故选A．
解：∵AB=AC，∴∠B=∠C；
又∵∠FDE=∠B，
∴∠BFD+∠BDF=∠BDF+∠CDE，
∴∠BFD=∠CDE，而∠B=∠C，
∴△BDF∽△CCED，
∴BD：CE=BF：DC，
而BD=2，CD=3，CE=4，
∴BF=1.5，
∵AB=AC=1+4=5，
∴AF=5-1.5=3.5．
故选A．
点评：该题主要考查了相似三角形的判定及其性质的应用问题；解题的关键是灵活运用相似三角形的判定及其性质来分析、判断、推理或解答．
练习册系列答案
相关题目
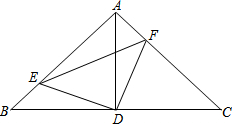如图，在Rt△ABC中，∠BAC=90°，点D为BC中点，点E、F分别为AB、AC上的点，且ED⊥FD．以线段BE、EF、FC为边能否构成一个三角形？若能，请判断此三角形的形状．
