题目内容
 如图,AD∥BC,∠DAC=70°,∠ACF=25°,∠EFC=135°,求证:EF∥BC.
如图,AD∥BC,∠DAC=70°,∠ACF=25°,∠EFC=135°,求证:EF∥BC.考点:平行线的判定与性质
专题:证明题
分析:由平行可得到∠DAC=∠ACB,结合条件可求得∠FCB=45°,可得∠EFC+∠FCB=180°,可判定EF∥BC.
解答:证明:
∵AD∥BC,
∴∠ACB=∠DAC=70°,
∵∠ACF=25°,
∴∠FCB=45°,
∴∠EFC+∠FCB=135°+45°=180°,
∴EF∥BC.
∵AD∥BC,
∴∠ACB=∠DAC=70°,
∵∠ACF=25°,
∴∠FCB=45°,
∴∠EFC+∠FCB=135°+45°=180°,
∴EF∥BC.
点评:本题主要考查平行线的性质和判定,掌握两直线平行的性质和判定是解题的关键,即①同位角相等?两直线平行,②内错角相等?两直线平行,③同旁内角互补?两直线平行.

练习册系列答案
相关题目
 以萝卜或马铃薯为主要材料,制作下列两组三视图所表示的几何体的立体模型,并画出你制作的这个模型.
以萝卜或马铃薯为主要材料,制作下列两组三视图所表示的几何体的立体模型,并画出你制作的这个模型.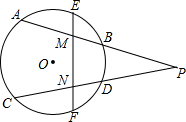 如图,已知圆O的弦AB、CD的延长线相交于点P,连接弧AB、弧CD的中点E、F分别交AB、CD于点M、N,求证:△PNM是等腰三角形.
如图,已知圆O的弦AB、CD的延长线相交于点P,连接弧AB、弧CD的中点E、F分别交AB、CD于点M、N,求证:△PNM是等腰三角形.