题目内容
13.分别画出下列各多边形的对角线,并观察图形完成下列问题:(1)试写出用n边形的边数n表示对角线总条数S的式子:S=$\frac{1}{2}$n(n-3).
(2)从十五边形的一个顶点可以引出12条对角线,十五边形共有90条对角线:
(3)如果一个多边形对角线的条数与它的边数相等,求这个多边形的边数.
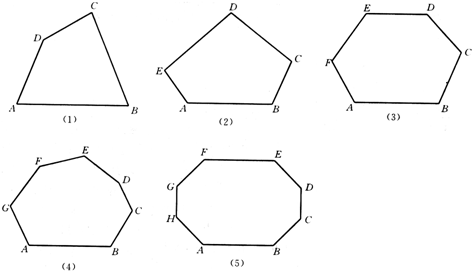
分析 (1)根据多边形对角线的条数的公式即可求解;
(2)根据多边形对角线的条数的公式代值计算即可求解;
(3)根据等量关系:一个多边形对角线的条数与它的边数相等,列出方程计算即可求解.
解答 解:(1)用n边形的边数n表示对角线总条数S的式子:S=$\frac{1}{2}$n(n-3);
(2)十五边形从一个顶点可引出对角线:15-3=12(条),共有对角线:$\frac{1}{2}$×15×(15-3)=90(条);
(3)设多边形有n条边,
则$\frac{1}{2}$n(n-3)=n,
解得n=5或n=0(应舍去).
故这个多边形的边数是5.
故答案为:S=$\frac{1}{2}$n(n-3);12,90.
点评 本题主要考查了多边形对角线的条数的公式总结,熟记公式对今后的解题大有帮助.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
4.下列说法不正确的是( )
| A. | $\frac{1}{25}$的平方根是±$\frac{1}{5}$ | B. | $\root{3}{-27}$=-3 | ||
| C. | (-0.1)2的平方根是±0.1 | D. | -9是81的算术平方根 |
1.下列方程属于一元二次方程的是( )
| A. | ax2+bx+c=0 | B. | x2-$\frac{2}{x}$=3 | C. | 4x2=81 | D. | (x+4)(x-2)=x2 |
5.函数y=$\sqrt{x+2}$中,自变量x的取值范围是( )
| A. | x>2 | B. | x<2 | C. | x≥-2 | D. | x≤-2 |
2.已知3a2x-1b2y与-3a-3yb3x+6是同类项,则x+y的值为( )
| A. | $\frac{1}{13}$ | B. | $\frac{31}{13}$ | C. | $\frac{15}{13}$ | D. | -$\frac{1}{13}$ |
3.下列图形中,是正方体表面展开图的是( )
| A. |  | B. |  | C. |  | D. |  |
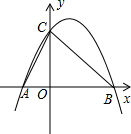 如图,在直角坐标系中,已知抛物线y=ax2+bx+2(a≠0)与x轴相交于点A(-1,0)和点B(4,0),与y轴的交点是C.
如图,在直角坐标系中,已知抛物线y=ax2+bx+2(a≠0)与x轴相交于点A(-1,0)和点B(4,0),与y轴的交点是C.