题目内容
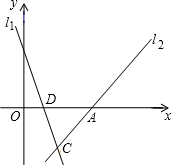 如图,已知直线l1:y=-3x+3与直线l2:y=mx-4m的图象的交点C 在第四象限,且点C到y轴的距离为2.
如图,已知直线l1:y=-3x+3与直线l2:y=mx-4m的图象的交点C 在第四象限,且点C到y轴的距离为2.(1)求直线l2的解析式;
(2)求△ADC的面积;
(3)在第一象限的角平分线上是否存在点P,使得△ADP的面积是△ADC的面积的2倍?如果存在,求出点P的坐标,如果不存在,请说明理由.
考点:两条直线相交或平行问题
专题:
分析:(1)由点C到y轴距离为2,可知C的横坐标为2,代入直线l1的解析式即可求得C的坐标;把C的坐标代入y=mx-4m,即可求得l2的解析式.
(2)根据直线的解析式求得A、D的坐标即可根据三角形的面积公式求得△ADC的面积;
(3)根据已知设点P为(x,x),根据△ADP的面积是△ADC的面积的2倍列出方程式,解方程即可求得P的坐标.
(2)根据直线的解析式求得A、D的坐标即可根据三角形的面积公式求得△ADC的面积;
(3)根据已知设点P为(x,x),根据△ADP的面积是△ADC的面积的2倍列出方程式,解方程即可求得P的坐标.
解答:解:(1)∵点C到y轴距离为2,点C在直线l1上,
∴y=-3×2+3=-3.
∴点C(2,-3),
∵点C在直线l2上,把C的坐标代入y=mx-4m,得m=
,
∴l2的解析式为y=
x-6;
(2)∵直线l1:y=-3x+3,
∴点D为(1,0),
∵直线l2为y=
x-6;
∴点A为(4,0),
∴△ADC的面积为
×(4-1)×3=
;
(3)∵点P在第一象限的角平分线上,
∴设点P为(x,x),
∵△ADP的面积是△ADC的面积的2倍等于9,
∴
×3x=9,解得x=6,
∴点P的坐标为(6,6).
∴y=-3×2+3=-3.
∴点C(2,-3),
∵点C在直线l2上,把C的坐标代入y=mx-4m,得m=
| 3 |
| 2 |
∴l2的解析式为y=
| 3 |
| 2 |
(2)∵直线l1:y=-3x+3,
∴点D为(1,0),
∵直线l2为y=
| 3 |
| 2 |
∴点A为(4,0),
∴△ADC的面积为
| 1 |
| 2 |
| 9 |
| 2 |
(3)∵点P在第一象限的角平分线上,
∴设点P为(x,x),
∵△ADP的面积是△ADC的面积的2倍等于9,
∴
| 1 |
| 2 |
∴点P的坐标为(6,6).
点评:本题考查了两条直线平行或相交问题,应用的知识点有:待定系数法求解析式,角的平分线的性质,三角形的面积等.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列说法中不正确的说法是( )
| A、对顶角相等 |
| B、等角的补角相等 |
| C、过任意一点都能画已知直线的垂线 |
| D、过任意一点都能画一条直线与已知直线平行 |
已知△ABC∽△DEF,且对应边AB:DE=2:3,则△ABC与△DEF的面积比是( )
| A、2:3 | ||||
B、
| ||||
| C、4:9 | ||||
| D、9:4 |
甲、乙两个同学在几次数学测量中,平均分都是86分,甲的方差是0.61,乙的方差是0.72.则下列说法中正确的是( )
| A、甲比乙的成绩稳定 |
| B、乙比甲的成绩稳定 |
| C、甲、乙两人的成绩一样稳定 |
| D、无法确定谁的成绩更稳定 |
新世纪商场周年庆时,小美将商场某一品牌商店的促销活动告诉小明后,小明假设该商品的标价为x元,并列出方程0.4(2x-100)=1000,则下列可能是小美告知小明促销内容的说法是( )
| A、买两件等值的商品可打4折,再少100元,最后才1000耶! |
| B、买两件等值的商品可打6折,再少100元,最后才1000耶! |
| C、买两件等值的商品可少100元,再打6折,最后才1000耶! |
| D、买两件等值的商品可少100元,再打4折,最后才1000耶! |
 如图,圆O是边长为6的正方形ABCD的内切圆,EF切圆0于P点,交AB、BC于点E,F,求△BEF的周长.
如图,圆O是边长为6的正方形ABCD的内切圆,EF切圆0于P点,交AB、BC于点E,F,求△BEF的周长.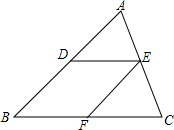 如图,在△ABC中,D、E分别是AB、AC的中点,过点E作EF∥AB,交BC于点F.当△ABC满足条件
如图,在△ABC中,D、E分别是AB、AC的中点,过点E作EF∥AB,交BC于点F.当△ABC满足条件 画出二次函数y=-x2+4x+5的图象,并根据图象回答下列问题:
画出二次函数y=-x2+4x+5的图象,并根据图象回答下列问题: