题目内容
 如图,圆O是边长为6的正方形ABCD的内切圆,EF切圆0于P点,交AB、BC于点E,F,求△BEF的周长.
如图,圆O是边长为6的正方形ABCD的内切圆,EF切圆0于P点,交AB、BC于点E,F,求△BEF的周长.考点:切线长定理
专题:
分析:设⊙O切AB于M,切BC于N,连接OM、ON,求出四边形BMON是正方形,求出BM=BN=3,根据切线长定理求出EM=EP,FP=FN,最后求出△BEF的周长=BM+BN,代入求出即可.
解答: 解:设⊙O切AB于M,切BC于N,连接OM、ON,
解:设⊙O切AB于M,切BC于N,连接OM、ON,
则∠OMB=∠ONB=90°,
∵四边形ABCD是正方形,
∴∠B=90°,
∵ON=OM,
∴四边形MBNO是正方形,
∵圆O是边长为6的正方形ABCD的内切圆,
∴BM=BN=OM=ON=
AB=
×6=3,
由切线长定理得:EM=EP,PF=FN,
∴△BEF的周长为BF+EF+BE
=BF+PF+PE+BE
=BF+FN+EM+BE
=BN+BM
=3+3
=6.
 解:设⊙O切AB于M,切BC于N,连接OM、ON,
解:设⊙O切AB于M,切BC于N,连接OM、ON,则∠OMB=∠ONB=90°,
∵四边形ABCD是正方形,
∴∠B=90°,
∵ON=OM,
∴四边形MBNO是正方形,
∵圆O是边长为6的正方形ABCD的内切圆,
∴BM=BN=OM=ON=
| 1 |
| 2 |
| 1 |
| 2 |
由切线长定理得:EM=EP,PF=FN,
∴△BEF的周长为BF+EF+BE
=BF+PF+PE+BE
=BF+FN+EM+BE
=BN+BM
=3+3
=6.
点评:本题考查了切线长定理,正方形的性质和判定,正方形的内切圆的应用,解此题的关键是求出△BEF的周长=BN+BM和求出BM的长,注意:从圆外一点引圆的两条切线,它们的切线长相等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列调查,比较适合用全面调查方式而不适合用抽样调查方式的是( )
| A、调查全省食品市场上某种食品的色素含量是否符合国家标准 |
| B、调查你所在班级全体学生的身高 |
| C、调查一批灯泡的使用寿命 |
| D、调查全国初中生每人每周的零花钱数 |
要在地球仪上确定深圳市的位置,需要知道的是( )
| A、高度 | B、经度 |
| C、纬度 | D、经度和纬度 |
 如图,在3×3的网格图中,在不添加其他线的情况下,不是正方形的矩形个数为( )
如图,在3×3的网格图中,在不添加其他线的情况下,不是正方形的矩形个数为( )| A、14个 | B、22个 |
| C、36个 | D、以上都不正确 |
若两个相似多边形的面积之比为1:4,则它们的周长之比为( )
| A、1:4 | B、1:2 |
| C、2:1 | D、1:16 |
在天气预报图上,有各种各样表示天气的符号,如图表示天气符号的图形中,不是轴对称图形的是( )
A、 冰雹 |
B、 雷阵雨 |
C、 晴 |
D、 大雪 |
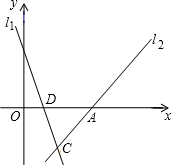 如图,已知直线l1:y=-3x+3与直线l2:y=mx-4m的图象的交点C 在第四象限,且点C到y轴的距离为2.
如图,已知直线l1:y=-3x+3与直线l2:y=mx-4m的图象的交点C 在第四象限,且点C到y轴的距离为2.