题目内容
15.在奥运会射击选手预选赛上,把甲、乙、丙三位选手各10次射击成绩的平均数和方差统计如表:| 选手 | 甲 | 乙 | 丙 |
| 平均数($\overline{x}$) | 9.3 | 9.3 | 9.3 |
| 方差(s2) | 0.026 | 0.015 | 0.032 |
分析 从统计表可以看出甲、乙、丙三位选手的平均数相同,进一步比较方差,方差小的数据比较稳定,由此解决问题即可.
解答 解:因为0.015<0.026<0.032,
即乙的方差<甲的方差<丙的方差,
因此射击成绩最稳定的选手是乙.
故答案为:乙.
点评 此题主要考查利用方差来判定数据的波动性,方差越小,数据越稳定.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
7.一个多边形的每个内角都相等,并且它的一个外角与一个内角的比为2:3,则这个多边形为( )
| A. | 三角形 | B. | 四边形 | C. | 五边形 | D. | 六边形 |
4. 如图,测得BD=120m,DC=60m,EC=50m,则河宽AB为( )
如图,测得BD=120m,DC=60m,EC=50m,则河宽AB为( )
 如图,测得BD=120m,DC=60m,EC=50m,则河宽AB为( )
如图,测得BD=120m,DC=60m,EC=50m,则河宽AB为( )| A. | 120m | B. | 100m | C. | 75m | D. | 25m |
10.已知反比例函数y=$\frac{10}{x}$,当2.5<x<5时,y的取值范围是( )
| A. | 2<y<4 | B. | 2.5<x<5 | C. | 5<y<10 | D. | y>10 |
6.为增强公民的节水意识,合理利用水资源,某市自1月1日起对市区民用水价格进行调整,实行阶梯式水价,调整后的收费价格如下表所示:
(1)若调价后每月支出的水费为y(元),每月的用水量为x(m3),求y与x之间的函数关系式并注明自变量的取值范围;
(2)若某用户2、3月份共用水16m3(3月份用水高于2月份用水量),共缴费48元,试问该用户2、3月份的用水量各是多少?
| 每月用水量 | 单价 |
| 不超过5m3的部分 | 2 |
| 超过5m3,不超,8m3部分 | 4 |
| 超出8m3部分 | 8 |
(2)若某用户2、3月份共用水16m3(3月份用水高于2月份用水量),共缴费48元,试问该用户2、3月份的用水量各是多少?
2.为求1+2+22+23+…+22015的值,可令S=1+2+22+23+…+22015,则2S=2+22+23+…+22016,因此2S-S=22016-1.仿照以上推理,计算出1+5+52+53+…+52015的值为( )
| A. | 52015-1 | B. | 52016-1 | C. | $\frac{{5}^{2015}-1}{4}$ | D. | $\frac{{5}^{2016}-1}{4}$ |
 如图中所示是一圆锥形的零件经过轴的剖面,它的腰长等于圆锥的母线长,底边长等于圆锥底面的直径,按图中表明的尺寸求这个零件的母线长为36.
如图中所示是一圆锥形的零件经过轴的剖面,它的腰长等于圆锥的母线长,底边长等于圆锥底面的直径,按图中表明的尺寸求这个零件的母线长为36.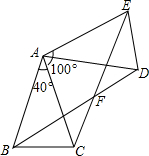 如图,△ABC中,AB=AC,∠BAC=40°,将△ABC绕点A按逆时针方向旋转100°,得到△ADE,连接BD和CE,BD与CE交于点F.
如图,△ABC中,AB=AC,∠BAC=40°,将△ABC绕点A按逆时针方向旋转100°,得到△ADE,连接BD和CE,BD与CE交于点F.