题目内容
7．一个多边形的每个内角都相等，并且它的一个外角与一个内角的比为2：3，则这个多边形为（ ）| A． | 三角形 | B． | 四边形 | C． | 五边形 | D． | 六边形 |
分析 此题要结合多边形的内角与外角的关系来寻求等量关系，构建方程求出每个外角．多边形外角和是固定的360°．
解答 解：设多边形的一个内角为x度，则一个外角为$\frac{2}{3}$x°，依题意得
x+$\frac{2}{3}$x=180°，即$\frac{5}{3}$x=180°，
x=108°．
360°÷（$\frac{2}{3}$×108°）=5．
故选C．
点评 此题考查多边形的内角与外角的关系、方程的思想．关键是记住多边形一个内角与外角互补和外角和的特征．
练习册系列答案
相关题目
19．要使代数式$\frac{1}{\sqrt{3x-1}}$有意义，则x的取值范围是（ ）
| A． | x＞$\frac{1}{3}$ | B． | x＜-$\frac{1}{3}$ | C． | x＜$\frac{1}{3}$ | D． | x＞-$\frac{1}{3}$ |
18．
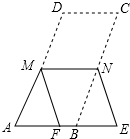如图，在?ABCD中，∠A=70°，将?ABCD折叠，使点D、C分别落在点F、E处（点F、E都在AB所在的直线上），折痕为MN，则∠AMF等于（ ）
如图，在?ABCD中，∠A=70°，将?ABCD折叠，使点D、C分别落在点F、E处（点F、E都在AB所在的直线上），折痕为MN，则∠AMF等于（ ）| A． | 70° | B． | 40° | C． | 30° | D． | 20° |
2．计算$\sqrt{8}$×$\sqrt{\frac{1}{2}}$+（$\sqrt{5}$）0的结果为（ ）
| A． | 2+$\sqrt{2}$ | B． | $\sqrt{2}$+1 | C． | 3 | D． | 5 |
已知：如图，?ABCD中，∠BCD的平分线交AB于点E，交侧的延长线于点F．
15．在奥运会射击选手预选赛上，把甲、乙、丙三位选手各10次射击成绩的平均数和方差统计如表：
则射击成绩最稳定的选手是乙（选填“甲”“乙”“丙”中的一个）
| 选手 | 甲 | 乙 | 丙 |
| 平均数（$\overline{x}$） | 9.3 | 9.3 | 9.3 |
| 方差（s2） | 0.026 | 0.015 | 0.032 |