题目内容
8．
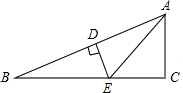如图，在Rt△ABC中，∠C=90°，AC=1，BC=3，AB的中垂线DE交BC于点E，连接AE，则AE的长$\frac{5}{3}$．
分析 由线段垂直平分线的性质可得AE=BE，设AE=x，则CE=3-x，在Rt△ACE中，由勾股定理可得到关于x的方程，可求得AE的长．
解答 解：∵E在线段AB的垂直平分线上，
∴AE=BE，
设AE=x，则BE=x，CE=BC-BE=3-x，
在Rt△ACE中，AC=1，由勾股定理可得AE2=AC2+CE2，
即x2=（3-x）2+12，解得x=$\frac{5}{3}$，
∴AE的长为$\frac{5}{3}$，
故答案为：$\frac{5}{3}$．
点评 本题主要考查线段垂直平分线的性质，掌握线段垂直平分线上的点到线段两端点的距离相等是解题的关键．注意方程思想的应用．
练习册系列答案
阅读快车系列答案
相关题目
3．已知$\frac{1}{x}$-$\frac{1}{y}$=3，则$\frac{2y+xy-2x}{x-y-xy}$的值为（ ）
| A． | -$\frac{7}{4}$ | B． | $\frac{7}{4}$ | C． | $\frac{4}{7}$ | D． | -$\frac{4}{7}$ |
如图，已知?ABCD中，E，F分别是AB，AD上的点，且BF=DE，BF与DE相交于点P，求证：PC平分∠BPD．