题目内容
13.写出下列两组式子的最简公分母:(1)$\frac{c}{ab}$,$\frac{a}{bc}$,$\frac{b}{ac}$:abc;
(2)$\frac{x}{1-a}$,$\frac{y}{(a-1)^{2}}$,$\frac{z}{(1-a)^{3}}$:(1-a)3.
分析 确定最简公分母的方法是:
(1)取各分母系数的最小公倍数;
(2)凡单独出现的字母连同它的指数作为最简公分母的一个因式;
(3)同底数幂取次数最高的,得到的因式的积就是最简公分母.
解答 解:(1)$\frac{c}{ab}$,$\frac{a}{bc}$,$\frac{b}{ac}$分母分别是ab、bc、ac,
故最简公分母是abc;
(2)$\frac{x}{1-a}$,$\frac{y}{(a-1)^{2}}$,$\frac{z}{(1-a)^{3}}$分母分别是1-a、(a-1)2、(1-a)3,
故最简公分母是(1-a)3;
故答案为abc,(1-a)3.
点评 本题考查了最简公分母,通分的关键是准确求出各个分式中分母的最简公分母,确定最简公分母的方法一定要掌握.

练习册系列答案
相关题目
5. 如图所示,AB是⊙O的直径,CD是弦,CD⊥AB于点E,则下列结论中不一定正确的是( )
如图所示,AB是⊙O的直径,CD是弦,CD⊥AB于点E,则下列结论中不一定正确的是( )
 如图所示,AB是⊙O的直径,CD是弦,CD⊥AB于点E,则下列结论中不一定正确的是( )
如图所示,AB是⊙O的直径,CD是弦,CD⊥AB于点E,则下列结论中不一定正确的是( )| A. | ∠COE=∠DOE | B. | CE=DE | C. | AC=AD | D. | OE=BE |
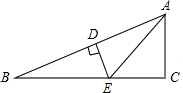 如图,在Rt△ABC中,∠C=90°,AC=1,BC=3,AB的中垂线DE交BC于点E,连接AE,则AE的长$\frac{5}{3}$.
如图,在Rt△ABC中,∠C=90°,AC=1,BC=3,AB的中垂线DE交BC于点E,连接AE,则AE的长$\frac{5}{3}$. 如图,已知∠ABC=∠ACB,BD平分∠ABC,CE平分∠ACB,F是BC延长线上一点,且∠DBC=∠F,求证:EC∥DF.
如图,已知∠ABC=∠ACB,BD平分∠ABC,CE平分∠ACB,F是BC延长线上一点,且∠DBC=∠F,求证:EC∥DF.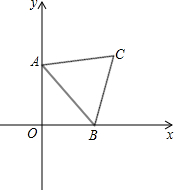 如图,直线y=-$\frac{3}{4}$x+6与坐标轴分别相交于点A、B.
如图,直线y=-$\frac{3}{4}$x+6与坐标轴分别相交于点A、B.