题目内容
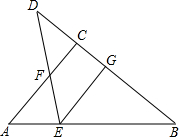 如图,在△ABC中,∠ACB=90°,D是BC延长线上一点,E是BD的垂直平分线与AB的交点,连接DE交AC于点F.求证:点E在AF的垂直平分线上.
如图,在△ABC中,∠ACB=90°,D是BC延长线上一点,E是BD的垂直平分线与AB的交点,连接DE交AC于点F.求证:点E在AF的垂直平分线上.考点:线段垂直平分线的性质
专题:证明题
分析:先根据EG是线段BD的垂直平分线得出∠DEG=∠BEG,再由∠ACB=90°可知AC∥EG,故∠AFE=∠DEG,∠A=∠BEG,所以∠A=∠AFE,由此即可得出结论.
解答:解:∵EG是线段BD的垂直平分线,
∴∠DEG=∠BEG,
∵∠ACB=90°,
∴AC∥EG,
∴∠AFE=∠DEG,∠A=∠BEG,
∴∠A=∠AFE,即点E在AF的垂直平分线上.
∴∠DEG=∠BEG,
∵∠ACB=90°,
∴AC∥EG,
∴∠AFE=∠DEG,∠A=∠BEG,
∴∠A=∠AFE,即点E在AF的垂直平分线上.
点评:本题考查的是线段垂直平分线的性质,熟知垂直平分线上任意一点,到线段两端点的距离相等是解答此题的关键.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
下列运算正确的是( )
| A、2a+3b=5ab |
| B、(-a-b)(b-a)=b2-a2 |
| C、a6÷a2=a3 |
| D、(a2b)2=a4b2 |
 若反比例函数
若反比例函数 已知:如图,在△ABC中,O是∠B、∠C外角的平分线的交点,那么点O在∠A的平分线上吗?为什么?
已知:如图,在△ABC中,O是∠B、∠C外角的平分线的交点,那么点O在∠A的平分线上吗?为什么? 如图,在平行四边形OABC中,OA=8,AB=6,∠AOC=120°,求点A,O,C,B各点的坐标.
如图,在平行四边形OABC中,OA=8,AB=6,∠AOC=120°,求点A,O,C,B各点的坐标.