题目内容
下列各式：
①y=2x2-3xz+5；②y=3-2x+5x2；③y=
+2x-3；④y=ax2+bx+c；⑤y=（2x-3）（3x-2）-6x2；⑥y=（m2+1）x2+3x-4（m为常数）；⑦y=m2x2+4x-3（m为常数）．
是二次函数的有（ ）
①y=2x2-3xz+5；②y=3-2x+5x2；③y=
| 1 |
| x2 |
是二次函数的有（ ）
| A、1个 | B、2个 | C、3个 | D、4个 |
考点：二次函数的定义
专题：
分析：根据二次函数的定义分别判断得出答案即可．
解答：解：①y=2x2-3xz+5，含有两个未知数，故此选项错误；
②y=3-2x+5x2，符合二次函数的定义，此选项正确；
③y=
+2x-3，含有分式，不是二次函数，故此选项错误；
④y=ax2+bx+c，a≠0，故此选项错误；
⑤y=（2x-3）（3x-2）-6x2=-10x+6，不是二次函数，故此选项错误；
⑥y=（m2+1）x2+3x-4（m为常数），符合二次函数定义，故此选项正确；
⑦y=m2x2+4x-3（m为常数），m≠0，不是二次函数，故此选项错误；
故是二次函数的有：2个．
故选：B．
②y=3-2x+5x2，符合二次函数的定义，此选项正确；
③y=
| 1 |
| x2 |
④y=ax2+bx+c，a≠0，故此选项错误；
⑤y=（2x-3）（3x-2）-6x2=-10x+6，不是二次函数，故此选项错误；
⑥y=（m2+1）x2+3x-4（m为常数），符合二次函数定义，故此选项正确；
⑦y=m2x2+4x-3（m为常数），m≠0，不是二次函数，故此选项错误；
故是二次函数的有：2个．
故选：B．
点评：此题主要考查了二次函数的定义，正确把握二次函数定义是解题关键．
练习册系列答案
阅读快车系列答案
相关题目
已知二次函数y=ax2+bx+c（a≠0）的图象如图，其对称轴为直线x=-1，给出下列结果：（1）b2＞4ac；（2）abc＞0；（3）2a+b=0；（4）a+b+c＞0；（5）a-b+c＜0．
则正确的结论是（ ）
| A、（1）（2）（3）（4） |
| B、（2）（4）（5） |
| C、（2）（3）（4） |
| D、（1）（4）（5） |
已知ax=bx，下列结论错误的是（ ）
| A、a=b | ||||
| B、ax+c=bx+c | ||||
| C、（a-b）x=0 | ||||
D、
|
下列代数式中，与-3a2b为同类项的是（ ）
| A、-3ab3 |
| B、3a2b2 |
| C、-ba2 |
| D、2ab2 |
下列多项式的分解因式，正确的是（ ）
| A、12xyz-9x2y2=3xyz（4-3xyz） |
| B、3a2y-3ay+6y=3y（a2-a+2） |
| C、-x2+xy-xz=-x（x2+y-z） |
| D、a2b+5ab-b=b（a2+5a） |
如图，在△ABC中，BP、CP分别是△ABC的外角∠DBC和∠ECB的平分线，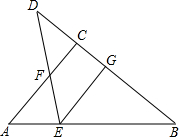
如图，在△ABC中，∠ACB=90°，D是BC延长线上一点，E是BD的垂直平分线与AB的交点，连接DE交AC于点F．求证：点E在AF的垂直平分线上．