题目内容
3.某商场试销一种成本为每件60元的服装,规定试销期间销售单价不低于成本单价,经试销发现,销售量y(件)与销售单价x(元)符合一次函数y=-x+140,该商场销售这种服装获得利润为w元.(1)求w与x之间的函数关系式;
(2)销售单价定为多少时,商场可获得最大利润?最大利润是多少元?
(3)若该商场想要获得不低于700元的利润,试确定销售单价x的范围.
分析 (1)根据利润=(售价-成本)×销售量列出函数关系式;
(2)直接利用配方法求出二次函数最值即可;
(3)令函数关系式W=700,解得x,然后进行讨论.
解答 解:(1)根据题意可得:
w=(x-60)y,
=(x-60)(-x+140),
=-x2+200x-8400,
=-(x-100)2+1600;
(2)∵w=-(x-100)2+1600,
a=-1<0,
∴当x=100时,w取最大值,最大值为1600,
∴销售单价定为100元时,商场可获得最大利润,最大利润是1600元;
(3)当w=700时,
-(x-100)2+1600=700,
解得:x1=70,x2=130,
∵抛物线w=(x-100)2+1600开口向下,
∴当70≤x≤130时,w≥750,
∴销售单价x的范围定为:70≤x≤130.
点评 本题主要考查二次函数的应用,根据利润=(售价-成本)×销售量列出函数关系式,求最值,运用二次函数解决实际问题,比较简单.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
13.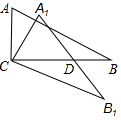 如图,Rt△ABC中,∠A=60°,将△ABC绕点C顺时针旋转得到△A1B1C,斜边A1B1与CB相交于点D,且DC=AC,则旋转角∠ACA1等于( )
如图,Rt△ABC中,∠A=60°,将△ABC绕点C顺时针旋转得到△A1B1C,斜边A1B1与CB相交于点D,且DC=AC,则旋转角∠ACA1等于( )
 如图,Rt△ABC中,∠A=60°,将△ABC绕点C顺时针旋转得到△A1B1C,斜边A1B1与CB相交于点D,且DC=AC,则旋转角∠ACA1等于( )
如图,Rt△ABC中,∠A=60°,将△ABC绕点C顺时针旋转得到△A1B1C,斜边A1B1与CB相交于点D,且DC=AC,则旋转角∠ACA1等于( )| A. | 20° | B. | 25° | C. | 30° | D. | 35° |
14.已知M(a,3)和N(4,b)关于y轴对称,则(a+b)2007的值为( )
| A. | 1 | B. | -1 | C. | 72007 | D. | -72007 |
11.比较-$\frac{1}{3}$,-$\frac{1}{4}$,$\frac{1}{6}$的大小,结果正确的是( )
| A. | $\frac{1}{6}<-\frac{1}{4}<-\frac{1}{3}$ | B. | $\frac{1}{6}<-\frac{1}{3}<-\frac{1}{4}$ | C. | $-\frac{1}{4}<-\frac{1}{3}<\frac{1}{6}$ | D. | $-\frac{1}{3}<-\frac{1}{4}<\frac{1}{6}$ |
15.下列说法中正确的个数是( )
①1是单项式;
②单项式-$\frac{ab}{2}$的系数是-1,次数是2;
③多项式x2+x-1的常数项是1;
④多项式x2+2xy+y2的次数是2.
①1是单项式;
②单项式-$\frac{ab}{2}$的系数是-1,次数是2;
③多项式x2+x-1的常数项是1;
④多项式x2+2xy+y2的次数是2.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
13.一次函数的图象经过点(-1,0)和点(0,3),则该一次函数的表达式为( )
| A. | y=3x+3 | B. | y=3x-3 | C. | y=-3x+3 | D. | y=-3x-3 |