题目内容
已知关于x的方程x+
+2(x+
)=1,求x+
+1的值.
| 1 |
| x2 |
| 1 |
| x |
| 1 |
| x |
考点:换元法解分式方程
专题:换元法
分析:可把方程中的x+
看成一个整体,设x+
=y,则原方程可化为y2+2y-3=0,然后运用配方法就可求出y+1即x+
+1的值.
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
解答:解:设x+
=y,则x2+
=(x+
)2-2=y2-2.
故原方程可化为y2-2+2y=1.
整理得:y2+2y-3=0.
则(y+1)2=4.
解得:y+1=±2.
即x+
+1=±2.
所以x+
+1的值为±2.
| 1 |
| x |
| 1 |
| x2 |
| 1 |
| x |
故原方程可化为y2-2+2y=1.
整理得:y2+2y-3=0.
则(y+1)2=4.
解得:y+1=±2.
即x+
| 1 |
| x |
所以x+
| 1 |
| x |
点评:本题考查了整体思想、转化思想、换元法、配方法等数学思想方法,是一道好题.

练习册系列答案
相关题目
已知关于x的一元二次方程(m-3)x2+4x+m2-9=0有一个根为0,则m为( )
| A、-3或3 | B、3 | C、-3 | D、0 |




 如图,在△ABC中,∠B与∠C的平分线相交于O点,过O点作MN∥BC交AB于M,交AC于N.若AB=12,BC=24,AC=18,则△AMN的周长为( )
如图,在△ABC中,∠B与∠C的平分线相交于O点,过O点作MN∥BC交AB于M,交AC于N.若AB=12,BC=24,AC=18,则△AMN的周长为( ) 如图,已知△ABC三个顶点的坐标分别为A(-2,3),B(-6,0),C(-1,0)
如图,已知△ABC三个顶点的坐标分别为A(-2,3),B(-6,0),C(-1,0)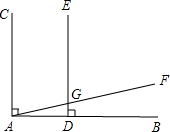 如图,已知AC⊥AB,ED⊥AB,∠CAF=78°,求∠DGF的度数.
如图,已知AC⊥AB,ED⊥AB,∠CAF=78°,求∠DGF的度数.