题目内容
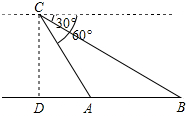 某日,正在我国南海海域作业的一艘大型渔船突然发生险情,相关部门接到求救信号后,立即调遣一架直升飞机和一艘刚在南海巡航的渔政船前往救援.当飞机到达距离海面3000米的高空C处,测得A处渔政船的俯角为60°,测得B处发生险情渔船的俯角为30°,请问:此时渔政船和渔船相距多远?(结果保留根号)
某日,正在我国南海海域作业的一艘大型渔船突然发生险情,相关部门接到求救信号后,立即调遣一架直升飞机和一艘刚在南海巡航的渔政船前往救援.当飞机到达距离海面3000米的高空C处,测得A处渔政船的俯角为60°,测得B处发生险情渔船的俯角为30°,请问:此时渔政船和渔船相距多远?(结果保留根号)考点:解直角三角形的应用-仰角俯角问题
专题:应用题
分析:在Rt△CDB中求出BD,在Rt△CDA中求出AD,继而可得AB,也即此时渔政船和渔船的距离.
解答:解:在Rt△CDA中,∠ACD=30°,CD=3000米,
∴AD=CDtan∠ACD=1000
米,
在Rt△CDB中,∠BCD=60°,
∴BD=CDtan∠BCD=3000
米,
∴AB=BD-AD=2000
米.
答:此时渔政船和渔船相距2000
米.
∴AD=CDtan∠ACD=1000
| 3 |
在Rt△CDB中,∠BCD=60°,
∴BD=CDtan∠BCD=3000
| 3 |
∴AB=BD-AD=2000
| 3 |
答:此时渔政船和渔船相距2000
| 3 |
点评:本题考查了解直角三角形的应用,解答本题的关键是熟练锐角三角函数的定义,能利用已知线段及锐角三角函数值表示未知线段.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目