题目内容
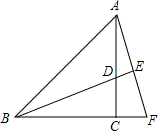 如图:△ABC中,AC=BC,∠ACB=90°,BD平分∠ABC且交AC于点D,将△BCD绕点C顺时针旋转到△ACF的位置,并延长BD交AF于点E.
如图:△ABC中,AC=BC,∠ACB=90°,BD平分∠ABC且交AC于点D,将△BCD绕点C顺时针旋转到△ACF的位置,并延长BD交AF于点E.①求证:△BAE∽△ADE;②若ED•BE=8,求BD的值.
考点:相似三角形的判定与性质
专题:
分析:①由∠ACB=90°可得∠DAE+∠F=∠EBF+∠F,可得∠DAE=∠EBF,又由角平分线可知∠ABE=∠EBF,可得∠DAE=∠ABE,且∠AEB=∠AED,可得结论;
②由①可知BE⊥AF,则有AE=EF,由条件可证明△ADE∽△BFE,可得
=
,可得AE2=DE•BE=8,可求得AE=2
,则BD=AF=4
.
②由①可知BE⊥AF,则有AE=EF,由条件可证明△ADE∽△BFE,可得
| DE |
| AE |
| AE |
| BE |
| 2 |
| 2 |
解答:①证明:∵∠ACB=90°,
∴∠DAE+∠F=∠EBF+∠F=90°,
∴∠DAE=∠EBF,
又∵BD平分∠ABC,
∴∠ABE=∠EBF,
∴∠DAE=∠ABE,且∠AEB=∠AED,
∴△BAE∽△ADE;
②解:∵∠DBC+∠BDC=90°,且∠DAAE=∠DBC,∠BDC=∠ADE,
∴∠DAE+∠ADE=90°,
∴AE=FE,
又∵在△BEF和△AED中,
∠DAE=∠EBF,∠AED=∠BEF,
∴△ADE∽△BFE,
∴
=
,
∴AE2=DE•BE=8,
∴AE=2
,
又∵由旋转的性质可得BD=AF,
∴BD=4
.
∴∠DAE+∠F=∠EBF+∠F=90°,
∴∠DAE=∠EBF,
又∵BD平分∠ABC,
∴∠ABE=∠EBF,
∴∠DAE=∠ABE,且∠AEB=∠AED,
∴△BAE∽△ADE;
②解:∵∠DBC+∠BDC=90°,且∠DAAE=∠DBC,∠BDC=∠ADE,
∴∠DAE+∠ADE=90°,
∴AE=FE,
又∵在△BEF和△AED中,
∠DAE=∠EBF,∠AED=∠BEF,
∴△ADE∽△BFE,
∴
| DE |
| AE |
| AE |
| BE |
∴AE2=DE•BE=8,
∴AE=2
| 2 |
又∵由旋转的性质可得BD=AF,
∴BD=4
| 2 |
点评:本题主要考查相似三角形的判定和性质,在第②问中证明△ADE∽△BFE求得AE的长是解题的关键.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
在抛物线y=2x2-3x+1上的点是( )
| A、(0,-1) | ||
B、(
| ||
| C、(-1,5) | ||
| D、(3,4) |
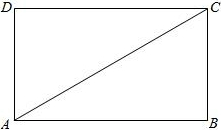 如图,矩形ABCD中,对角线AC=10,BC=5
如图,矩形ABCD中,对角线AC=10,BC=5 如图,∠AOB=∠COD=90°,∠AOD=140°,则∠BOC=
如图,∠AOB=∠COD=90°,∠AOD=140°,则∠BOC=