题目内容
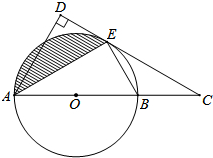 如图,已知AB为⊙O的直径,C是AB延长线上一点,CD与⊙O相切于点E,AD⊥CD,垂足为D.
如图,已知AB为⊙O的直径,C是AB延长线上一点,CD与⊙O相切于点E,AD⊥CD,垂足为D.(1)求证:AE平分∠DAC;
(2)若AB=6,∠ABE=60°,求图中阴影部分的面积.
考点:切线的性质,扇形面积的计算
专题:
分析:(1)连接OE,可证得OE∥AD,则∠DAE=∠AEO=∠EAO,可得结论;
(2)由条件求得∠AOE=120°,容易求得△AOE和扇形AOE的面积,利用面积差可求得阴影部分的面积.
(2)由条件求得∠AOE=120°,容易求得△AOE和扇形AOE的面积,利用面积差可求得阴影部分的面积.
解答: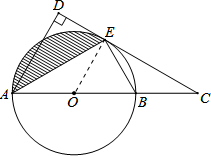 (1)证明:如图,连接OE,
(1)证明:如图,连接OE,
∵DC为切线,
∴OE⊥CD,且AD⊥CD,
∴OE∥AD,
∴∠DAE=∠AEO,
∵OE=OA,
∴∠AEO=∠EAO,
∴∠DAE=∠EAO,
即AE平分∠DAC;
(2)解:∵∠ABE=60°,
∴∠AOE=120°,
且AB=6,则OA=OB=BE=3,在Rt△ABE中可求得AE=3
,
∴S扇形AOE=
π•OA2=3π,S△AOE=
S△ABE=
×
AE•BE=
,
∴S阴影=S扇形AOE-S△AOE=3π-
.
 (1)证明:如图,连接OE,
(1)证明:如图,连接OE,∵DC为切线,
∴OE⊥CD,且AD⊥CD,
∴OE∥AD,
∴∠DAE=∠AEO,
∵OE=OA,
∴∠AEO=∠EAO,
∴∠DAE=∠EAO,
即AE平分∠DAC;
(2)解:∵∠ABE=60°,
∴∠AOE=120°,
且AB=6,则OA=OB=BE=3,在Rt△ABE中可求得AE=3
| 3 |
∴S扇形AOE=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
9
| ||
| 4 |
∴S阴影=S扇形AOE-S△AOE=3π-
9
| ||
| 4 |
点评:本题主要考查切线的性质及扇形面积的计算,掌握切线的性质及扇形的面积公式是解题的关键.注意题目中有切点,则连接圆心和切点是常用的辅助线.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
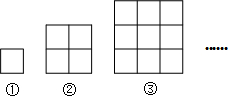 如图,每一幅图中均含有若干个正方形,第①幅图中含有1个正方形;第②幅图中含有5个正方形;按这样的规律下去,则第⑥幅图中含有正方形的个数为( )
如图,每一幅图中均含有若干个正方形,第①幅图中含有1个正方形;第②幅图中含有5个正方形;按这样的规律下去,则第⑥幅图中含有正方形的个数为( )| A、55 | B、78 | C、91 | D、140 |
如图,有理数a,b在数轴上的位置如图所示:

则在a+b,b-2a,|b|-|a|,|a-b|,|a+2|,-|b-4|中负数共有( )

则在a+b,b-2a,|b|-|a|,|a-b|,|a+2|,-|b-4|中负数共有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
 如图,锐角三角形ABC的两条高BE、CD相交于点O,且OB=OC
如图,锐角三角形ABC的两条高BE、CD相交于点O,且OB=OC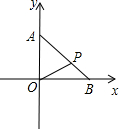 如图,点B,A分别在x,y轴的正半轴上,AB=m,且AP:PB=2:1,点B在x轴的正半轴上移动,线段AB的长保持不变.
如图,点B,A分别在x,y轴的正半轴上,AB=m,且AP:PB=2:1,点B在x轴的正半轴上移动,线段AB的长保持不变. 如图,∠AOB=∠COD=90°,∠AOD=140°,则∠BOC=
如图,∠AOB=∠COD=90°,∠AOD=140°,则∠BOC=