题目内容
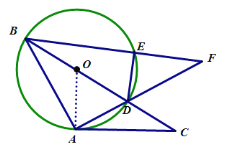
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 在
在![]() 上,以
上,以![]() 为半径的
为半径的![]() 经过点
经过点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .
.
(1)求证:![]() 为
为![]() 的切线;
的切线;
(2)延长![]() 到点
到点![]() ,连接
,连接![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,若
,若![]() ,求
,求![]() 的半径.
的半径.
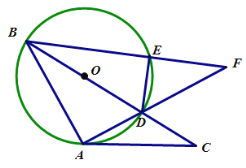
【答案】(1)见解析;(2)![]()
【解析】
(1)连接OA,利用等边对等角证得∠DAC=∠OAB,利用圆周角定理证得∠BAD=90![]() ,继而证得∠OAC=90
,继而证得∠OAC=90![]() ,从而证得结论;
,从而证得结论;
(2)在Rt![]() ABF中,求得AB,即可求得AC的长,利用三角形内角和定理可求得∠C=30
ABF中,求得AB,即可求得AC的长,利用三角形内角和定理可求得∠C=30![]() ,利用正切函数即可求解.
,利用正切函数即可求解.
(1)连接![]() .
.
∵AB=AC,
∴∠ABC=∠C,
∵AD=DC,
∴∠DAC=∠C,
∴∠ABC=∠DAC,
∵OA=OD,
∴∠OAD=∠ODA,
∵BD是直径
∴∠BDA=90![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() 是
是![]() 的半径,
的半径,
∴![]() 为
为![]() 的切线.
的切线.
(2)在![]() 中,由勾股定理得:
中,由勾股定理得:![]() ,
,
∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
在![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 的半径为
的半径为![]() .
.

练习册系列答案
相关题目
【题目】某礼品店从文化用品市场批发甲、乙、丙三种礼品(每种礼品都有),各礼品的数量和批发单价列表如下:
甲 | 乙 | 丙 | |
数量(个) |
|
|
|
批发单价(元) |
|
|
|
|
![]() 当
当![]() 时,若这三种礼品共批发
时,若这三种礼品共批发![]() 个,甲礼品的总价不低于丙礼品的总价,求
个,甲礼品的总价不低于丙礼品的总价,求![]() 的最小值.
的最小值.
![]() 已知该店用
已知该店用![]() 元批发了这三种礼品,且
元批发了这三种礼品,且![]() .
.
![]() 当
当![]() 时,若批发这三种礼品的平均单价为
时,若批发这三种礼品的平均单价为![]() 元/个,求
元/个,求![]() 的值.
的值.
![]() 当
当![]() 时,若该店批发了
时,若该店批发了![]() 个丙礼品,且
个丙礼品,且![]() 为正整数,求
为正整数,求![]() 的值.
的值.