题目内容
6.阅读下面材料并完成填空,你能比较两个数20072008和20082007的大小吗?为了解决这个问题,先把问题一般化,即比较nn+1和(n+1)n的大小(n≥1的整数),然后,从分析这些简单情形入手,从中发现规律,经过归纳,猜想出结论.(1)通过计算,比较下列各组两个数的大小(在横线上填>、=、<号)
①12<21; ②23<32; ③34>43; ④45>54; ⑤56>65;
…
(2)从第(1)小题的结果经过归纳,可以猜想,nn+1和(n+1)n的大小关系是什么?
(3)根据上面归纳猜想得到的一般结论,可以猜想得到20072008>20082007(填>、=、<).
分析 (1)根据乘方的意义求出每个式子的结果,再比较即可.
(2)根据(1)的结果即可得出结论.
(3)根据(2)中结论比较即可
解答 (1)①12<21,
故答案为:<.
②23<32,
故答案为:<.
③34>43,
故答案为:>.
④45>54,
故答案为:>.
⑤56>65,
故答案为:>;
(2)由(1)可知,当n=1或2时,nn+1<(n+1)n,
当n≥3时,nn+1>(n+1)n;
(3)∵2007>3,2008>3,
∴20072008>20082007.
故答案为:>.
点评 本题考查了有理数的乘方和有理数的大小比较的应用,关键是能得出规律.

练习册系列答案
相关题目
16.某地区每升高100米,气温降低0.6℃,测得地面气温为0℃,问550米的高空的气温为多少摄氏度?( )
| A. | 33℃ | B. | -33℃ | C. | 3.3℃ | D. | -3.3℃ |
17.用配方法解一元二次方程x2+6x-8=0时可配方得( )
| A. | (x-3)2=17 | B. | (x+3)2=17 | C. | (x-3)2=1 | D. | (x-3)2=-1 |
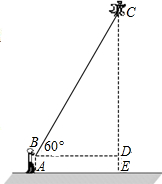 小明站在A处放风筝,风筝飞到C处时的线长为BC=20米,这时测得∠CBD=60°,若牵引底端B与地面的距离AB=1.5米,求此时风筝离地面的高度CE.
小明站在A处放风筝,风筝飞到C处时的线长为BC=20米,这时测得∠CBD=60°,若牵引底端B与地面的距离AB=1.5米,求此时风筝离地面的高度CE. 某汽车离开某城市的距离y(km)与行驶时间t(h)之间的关系式为y=kt+30,其图象如图所示.
某汽车离开某城市的距离y(km)与行驶时间t(h)之间的关系式为y=kt+30,其图象如图所示.