题目内容
1.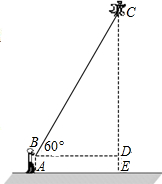 小明站在A处放风筝,风筝飞到C处时的线长为BC=20米,这时测得∠CBD=60°,若牵引底端B与地面的距离AB=1.5米,求此时风筝离地面的高度CE.
小明站在A处放风筝,风筝飞到C处时的线长为BC=20米,这时测得∠CBD=60°,若牵引底端B与地面的距离AB=1.5米,求此时风筝离地面的高度CE.
分析 根据直角三角形的性质求出BD的长,根据勾股定理求出CD的长,根据CE=CD+DE求出答案.
解答 解:∵∠CDB=90°,∠CBD=60°,
∴∠C=30°,
∴BD=$\frac{1}{2}$BC=10米,
∴CD=$\sqrt{B{C}^{2}-B{D}^{2}}$=10$\sqrt{3}$米,
∴CE=CD+DE=10$\sqrt{3}$+$\frac{3}{2}$米,
答:此时风筝离地面的高度CE为10$\sqrt{3}$+$\frac{3}{2}$米.
点评 本题考查的是勾股定理的应用,关键是从题中抽象出勾股定理这一数学模型,画出准确的示意图.领会数形结合的思想的应用.

练习册系列答案
相关题目
10.下列函数中一定是二次函数的是( )
| A. | y=(x+3)2-x2 | B. | y=x2-$\frac{1}{x}$ | C. | y=ax2+bx+c | D. | y=(2x-1)(x+2) |