题目内容
5.计算下列各题:(1)11-13+18
(2)-30×($\frac{1}{2}$-$\frac{2}{3}$+$\frac{4}{5}$)
(3)-22+$\root{3}{27}$÷(-2)×$\sqrt{16}$
(4)先化简,再求值:-(a2+2ab)+[a2-2(ab-2)],其中a=-$\frac{3}{4}$,b=$\frac{4}{3}$.
分析 (1)依据加减法则计算即可;
(2)依据乘法分配律计算即可;
(3)先依据立方根和算术平方根的性质进行化简,然后依据实数的运算法则和运算顺序进行计算即可;
(4)先去括号、合并同类项,最后将a、b的值代入求解即可.
解答 解:(1)原式=11+18-13=16;
(2)原式=-15+20-24=-19;
(3)原式=-4+3×(-$\frac{1}{2}$)×4=-4+(-6)=-10;
(4)原式=-a2-2ab+a2-2ab+4=-4ab+4.
当a=-$\frac{3}{4}$,b=$\frac{4}{3}$时,原式=-4×1+4=0.
点评 本题主要考查的是实数的运算,整式的化简求值,熟练掌握相关法则是解题的关键.

练习册系列答案
相关题目
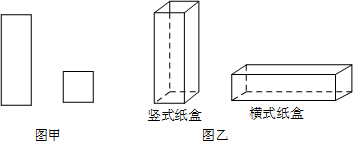
15.某工厂用如图甲所示的长方形和正方形纸板,做成如图乙所示的竖式与横式两种长方体形状的无盖纸盒.
(1)现有正方形纸板162张,长方形纸板340张.若要做两种纸盒共100个,设做竖式纸盒x个.
①根据题意,完成以下表格:
②按两种纸盒的生产个数来分,有哪几种生产方案?
(1)现有正方形纸板162张,长方形纸板340张.若要做两种纸盒共100个,设做竖式纸盒x个.
①根据题意,完成以下表格:
| 竖式纸盒(个) | 横式纸盒(个) | |
| 正方形纸板(张) | x | 2(100-x) |
| 长方形纸板(张) | 4x | 3(100-x) |

13.下列命题中,属于真命题的是( )
| A. | 两个锐角的和是锐角 | B. | 在同一平面内,如果a⊥b,b⊥c,则a⊥c | ||
| C. | 同位角相等 | D. | 在同一平面内,如果a∥b,b∥c,则a∥c |
10.下列实数中,是有理数的为( )
| A. | $\sqrt{2}$ | B. | $\root{3}{4}$ | C. | π | D. | $\frac{1}{2}$ |
17.点P是△ABC边AB上一点(AB>AC),下列条件不一定能使△ACP∽△ABC的是( )
| A. | ∠ACP=∠B | B. | ∠APC=∠ACB | C. | $\frac{AC}{AB}=\frac{AP}{AC}$ | D. | $\frac{PC}{BC}=\frac{AC}{AB}$ |
 如图所示,转盘被等分成六个扇形,并在上面依次写上数字1、2、3、4、5、6.
如图所示,转盘被等分成六个扇形,并在上面依次写上数字1、2、3、4、5、6. 如图,在△ABC中,D、E分别是AC、AB边上的点,若要△ADE与△ABC相似,则需要添加的一个条件是∠ADE=∠B.
如图,在△ABC中,D、E分别是AC、AB边上的点,若要△ADE与△ABC相似,则需要添加的一个条件是∠ADE=∠B.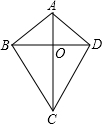 如图所示,AC、BD相交于点O,△ABO≌△ADO,下列结论正确的个数是( )
如图所示,AC、BD相交于点O,△ABO≌△ADO,下列结论正确的个数是( )