题目内容
1.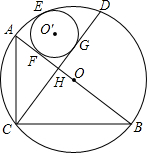 如图,已知⊙O的直径AB=6,弦CD⊥AB于H,⊙O′分别切⊙O、AB、CD于点E、F、G,则当⊙O′的半径取得最大值时,边BC的长度是( )
如图,已知⊙O的直径AB=6,弦CD⊥AB于H,⊙O′分别切⊙O、AB、CD于点E、F、G,则当⊙O′的半径取得最大值时,边BC的长度是( )| A. | 3.5 | B. | 3 | C. | 2.5 | D. | 2 |
分析 设⊙O′的半径为r,BC=x,可证明BC2=BH•BA,连接O′F,在Rt△OO′F中由勾股定理可得到r关于x的二次函数,再利用二次函数的性质可求得BC的长.
解答 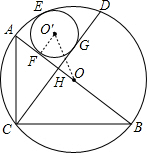 解:设⊙O′的半径为r,BC=x,
解:设⊙O′的半径为r,BC=x,
∵AB为⊙O的直径,
∴∠C=90°,
又AB⊥CD,
∴BC2=BH•BA=6(BF-FH)=6(BF-r),
如图,连接O′F,OO′,
∵AB为⊙O′的切线,
∴△OO′F为直角三角形,
∴O′O2-O′F2=OF2,
∴(3-r)2-r2=(BF-3)2,
∴BF2=6(BF-r),
∴BC=BF,
∴BC2=6(BC-r),即x2=6(x-r),
∴r=-$\frac{1}{6}$x2+x=-$\frac{1}{6}$(x-3)2+$\frac{3}{2}$,
∴当x=3时,⊙O′的半径取得最大值,
即BC的长为3,
故选B.
点评 本题主要考查切线的性质及圆与圆的位置关系、直角三角形的性质、二次函数的性质等知识的综合应用.由条件证明BC=BF,从而找到BC与⊙O′的半径的函数关系式是解题的关键.注意方程思想的应用.

练习册系列答案
相关题目
 如图,△ABC中,P为BC边上的一点,PD∥AC,PE∥AB,说明∠DPE=∠BAC的理由.
如图,△ABC中,P为BC边上的一点,PD∥AC,PE∥AB,说明∠DPE=∠BAC的理由.
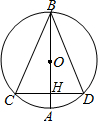 如图,AB是圆O的直径,CD为弦,AB⊥CD,垂足为H,连接BC、BD.
如图,AB是圆O的直径,CD为弦,AB⊥CD,垂足为H,连接BC、BD.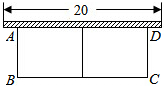 如图,有长为30m的篱笆,一面利用墙(墙的最大可用长度为20m),围成中间隔有一道篱笆(平行于AB)的矩形花圃ABCD.设花圃的一边AB为x(m).
如图,有长为30m的篱笆,一面利用墙(墙的最大可用长度为20m),围成中间隔有一道篱笆(平行于AB)的矩形花圃ABCD.设花圃的一边AB为x(m).