题目内容
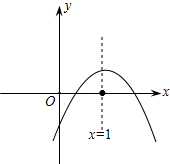 二次函数y=ax2+bx+c的图象如图所示,下列结论:①b>0,②c<0,③b2-4ac>0,④a+b+c>0,⑤4a+2b+c>0.其中正确的有( )
二次函数y=ax2+bx+c的图象如图所示,下列结论:①b>0,②c<0,③b2-4ac>0,④a+b+c>0,⑤4a+2b+c>0.其中正确的有( )| A、2个 | B、3个 | C、4个 | D、5个 |
考点:二次函数图象与系数的关系
专题:数形结合
分析:观察图象:根据二次函数图象与系数的关系由抛物线开口向下得a<0;由抛物线的对称轴在y轴的右侧得到a、b异号,则b>0;由抛物线与y轴的交点在x轴下方得到c<0;由抛物线与x轴有两个交点得到△>0,即b2-4ac>0;当x=1时,y>0,即a+b+c>0;由对称轴为直线x=1,而抛物线与x轴的一个交点在点(0,0)与(1,0)之间,利用抛物线的对称性得到抛物线与x轴的另一个交点在点(1,0)与(2,0)之间,则当x=2时,y<0,即4a+2b+c<0.
解答:解:∵抛物线开口向下,
∴a<0;
又∵抛物线的对称轴在y轴的右侧,
∴x=-
>0,
∴b>0,所以①正确;
∵抛物线与y轴的交点在x轴下方,
∴c<0,所以②正确;
∵抛物线与x轴有两个交点,
∴△>0,即b2-4ac>0,所以③正确;
当x=1时,y>0,即a+b+c>0,所以④正确;
∵对称轴为直线x=1,而抛物线与x轴的一个交点在点(0,0)与(1,0)之间,
∴抛物线与x轴的另一个交点在点(1,0)与(2,0)之间,
∴当x=2时,y<0,即4a+2b+c<0,所以⑤不正确.
故选C.
∴a<0;
又∵抛物线的对称轴在y轴的右侧,
∴x=-
| b |
| 2a |
∴b>0,所以①正确;
∵抛物线与y轴的交点在x轴下方,
∴c<0,所以②正确;
∵抛物线与x轴有两个交点,
∴△>0,即b2-4ac>0,所以③正确;
当x=1时,y>0,即a+b+c>0,所以④正确;
∵对称轴为直线x=1,而抛物线与x轴的一个交点在点(0,0)与(1,0)之间,
∴抛物线与x轴的另一个交点在点(1,0)与(2,0)之间,
∴当x=2时,y<0,即4a+2b+c<0,所以⑤不正确.
故选C.
点评:本题考查了二次函数图象与系数的关系:二次函数y=ax2+bx+c(a≠0)的图象为一条抛物线,当a>0,抛物线的开口向上,在对称轴x=-
的左侧,y随x的增大而减小,在对称轴x=-
的右侧,y随x的增大而增大;当a<0,抛物线的开口向下,当x=-
时,函数值最大;抛物线与y轴的交点坐标为(0,c);当△=b2-4ac>0,抛物线与x轴有两个交点.
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |

练习册系列答案
相关题目
已知一元二次方程x2+mx+3=0配方后为(x+n)2=22,那么一元二次方程x2-mx-3=0配方后为( )
| A、(x+5)2=28 |
| B、(x+5)2=19或(x-5)2=19 |
| C、(x-5)2=19 |
| D、(x+5)2=28或(x-5)2=28 |
若|2007-m|+
=m,则m-20072=( )
| m-2008 |
| A、2007 |
| B、2008 |
| C、20082 |
| D、-20082 |
下列运算正确的是( )
| A、a3-a2=a |
| B、x6÷x2=x3 |
| C、(x3)2=x6 |
| D、a5•a2=a10 |
 如图,△ABC是等腰直角三角形,AC=BC,D是AC的中点,设∠ABD为α,那么tanα的值为( )
如图,△ABC是等腰直角三角形,AC=BC,D是AC的中点,设∠ABD为α,那么tanα的值为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
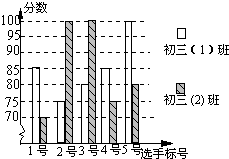 某中学开展“八荣八耻”演讲比赛活动,初三(1)班、(2)班根据初赛成绩各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩如图所示.
某中学开展“八荣八耻”演讲比赛活动,初三(1)班、(2)班根据初赛成绩各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩如图所示.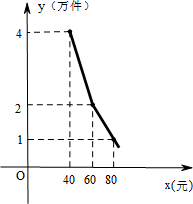 ,该产品每月销售量y(万件)与销售单价x(元)之间的函数关系如图所示.
,该产品每月销售量y(万件)与销售单价x(元)之间的函数关系如图所示.