题目内容
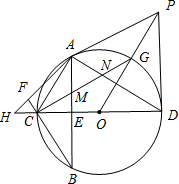 如图,CD为⊙O的直径,弦AB⊥CD于E,OP∥AC,且PD⊥CD,AF⊥BF交DC的延长线于H,连CG,分别交AB、AD于M、N.
如图,CD为⊙O的直径,弦AB⊥CD于E,OP∥AC,且PD⊥CD,AF⊥BF交DC的延长线于H,连CG,分别交AB、AD于M、N.(1)求证:PA为⊙O的切线.
(2)若AM=2EM,AN=
| 4 |
| 3 |
| 2 |
考点:切线的判定,全等三角形的判定与性质,三角形中位线定理,垂径定理,相似三角形的判定与性质
专题:几何综合题
分析:(1)连接OA,欲证PA为⊙O的切线,只需证明OA⊥PA即可;
(2)AM=2EM,且CM是角平分线,所以AC:CE=2:1,所以∠CAE=30°,ND:AN=2:1,从而可求AD长度,然后解直角三角形即可求得⊙O的直径.
(2)AM=2EM,且CM是角平分线,所以AC:CE=2:1,所以∠CAE=30°,ND:AN=2:1,从而可求AD长度,然后解直角三角形即可求得⊙O的直径.
解答: 解:(1)证明:∵CD为⊙O的直径,
解:(1)证明:∵CD为⊙O的直径,
∴∠CAD=90°(直径所对的圆周角是直角),
∴CA⊥DA;
又∵OP∥AC,
∴OP⊥AD,
∴OP垂直平分AD(垂径定理);
∵OA=OD(⊙O的半径),
∴∠AOP=∠DOP(等腰三角形“三线合一”);
在△AOP和△DOP中,
,
∴△AOP≌△DOP(SAS),
∴∠PAO=∠PDO(全等三角形的对应角相等);
∵PD⊥CD,
∴∠PAO=∠PDO=90°,∴OA⊥PA,
∵OA是⊙O的半径,
∴PA为⊙O的切线;
(2)由(1)中的AD⊥OP知,
=
,
∴∠ACG=∠DCG(等弧所对的圆周角相等),
∴
=
,
=
.
由∵AM=2EM(已知),
∴
=
,
=
,
∴∠CAE=30°(直角三角形中30°所对的直角边是斜边的一半),
∴∠ACE=60°.
∵OC=OA,
∴△OAC是等边三角形,
∴AC=OA=r,
∴
=
=
=
,
解得,r=
,即⊙O的半径是
.
 解:(1)证明:∵CD为⊙O的直径,
解:(1)证明:∵CD为⊙O的直径,∴∠CAD=90°(直径所对的圆周角是直角),
∴CA⊥DA;
又∵OP∥AC,
∴OP⊥AD,
∴OP垂直平分AD(垂径定理);
∵OA=OD(⊙O的半径),
∴∠AOP=∠DOP(等腰三角形“三线合一”);
在△AOP和△DOP中,
|
∴△AOP≌△DOP(SAS),
∴∠PAO=∠PDO(全等三角形的对应角相等);
∵PD⊥CD,
∴∠PAO=∠PDO=90°,∴OA⊥PA,
∵OA是⊙O的半径,
∴PA为⊙O的切线;
(2)由(1)中的AD⊥OP知,
 |
| AG |
 |
| DG |
∴∠ACG=∠DCG(等弧所对的圆周角相等),
∴
| AC |
| AM |
| CE |
| ME |
| AC |
| AN |
| CD |
| DN |
由∵AM=2EM(已知),
∴
| CE |
| AC |
| 1 |
| 2 |
| AN |
| DN |
| 1 |
| 2 |
∴∠CAE=30°(直角三角形中30°所对的直角边是斜边的一半),
∴∠ACE=60°.
∵OC=OA,
∴△OAC是等边三角形,
∴AC=OA=r,
∴
| AC |
| AN |
| CD |
| DN |
| r | ||||
|
| 2r | ||||||
|
解得,r=
4
| ||
| 3 |
4
| ||
| 3 |
点评:本题综合考查了切线的判定、全等三角形的判定与性质以及垂径定理等知识点.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.

练习册系列答案
相关题目
 有一种皮球是由40块黑白相间的牛皮缝制而成的(如图),黑皮可看作五边形,白皮可看作六边形,每块黑皮的周围都是白皮,而每块白皮有三条边和黑皮边在一起,则白皮有( )
有一种皮球是由40块黑白相间的牛皮缝制而成的(如图),黑皮可看作五边形,白皮可看作六边形,每块黑皮的周围都是白皮,而每块白皮有三条边和黑皮边在一起,则白皮有( )| A、16块 | B、20块 |
| C、25块 | D、26块 |
已知一元二次方程x2+mx+3=0配方后为(x+n)2=22,那么一元二次方程x2-mx-3=0配方后为( )
| A、(x+5)2=28 |
| B、(x+5)2=19或(x-5)2=19 |
| C、(x-5)2=19 |
| D、(x+5)2=28或(x-5)2=28 |
若|2007-m|+
=m,则m-20072=( )
| m-2008 |
| A、2007 |
| B、2008 |
| C、20082 |
| D、-20082 |
下列运算正确的是( )
| A、a3-a2=a |
| B、x6÷x2=x3 |
| C、(x3)2=x6 |
| D、a5•a2=a10 |
 如图,△ABC是等腰直角三角形,AC=BC,D是AC的中点,设∠ABD为α,那么tanα的值为( )
如图,△ABC是等腰直角三角形,AC=BC,D是AC的中点,设∠ABD为α,那么tanα的值为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
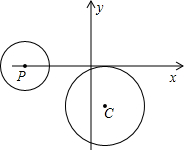 如图,⊙C与x轴相切,点C的坐标为(1,-3).点P在x轴上滑动,当半径为2的⊙P与⊙C外切时,点P的横坐标为
如图,⊙C与x轴相切,点C的坐标为(1,-3).点P在x轴上滑动,当半径为2的⊙P与⊙C外切时,点P的横坐标为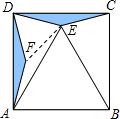 已知:E是正方形ABCD内一点,且∠ECD=∠EDC=15°,求证:△ABE是等边三角形,小萍同学灵活运用全等变换,将△ECD进行旋转与翻折,使△ECD≌△FAD,巧妙地解答了此题.请按照小萍的思路,探究并解答下列问题:
已知:E是正方形ABCD内一点,且∠ECD=∠EDC=15°,求证:△ABE是等边三角形,小萍同学灵活运用全等变换,将△ECD进行旋转与翻折,使△ECD≌△FAD,巧妙地解答了此题.请按照小萍的思路,探究并解答下列问题: 如图所示,在直角坐标系中,矩形OABC的顶点B的坐标为(12,5),直线
如图所示,在直角坐标系中,矩形OABC的顶点B的坐标为(12,5),直线