题目内容
某超市用3000元购进某种干果销售，由于销售状况良好，超市又调拨9000元资金购进该种干果，但这次的进价比第一次的进价提高了20%，购进干果数量是第一次的2倍还多300千克，如果超市按每千克9元的价格出售，当大部分干果售出后，余下的600千克按售价的8折售完．
（1）该种干果的第一次进价是每千克多少元？
（2）超市销售这种干果共盈利多少元？
（1）该种干果的第一次进价是每千克多少元？
（2）超市销售这种干果共盈利多少元？
考点：分式方程的应用
专题：销售问题
分析：（1）设该种干果的第一次进价是每千克x元，则第二次进价是每千克（1+20%）x元．根据第二次购进干果数量是第一次的2倍还多300千克，列出方程，解方程即可求解；
（2）根据利润=售价-进价，可求出结果．
（2）根据利润=售价-进价，可求出结果．
解答：解：（1）设该种干果的第一次进价是每千克x元，则第二次进价是每千克（1+20%）x元，
由题意，得
=2×
+300，
解得x=5，
经检验x=5是方程的解．
答：该种干果的第一次进价是每千克5元；
（2）[
+
-600]×9+600×9×80%-（3000+9000）
=（600+1500-600）×9+4320-12000
=1500×9+4320-12000
=13500+4320-12000
=5820（元）．
答：超市销售这种干果共盈利5820元．
由题意，得
| 9000 |
| (1+20%)x |
| 3000 |
| x |
解得x=5，
经检验x=5是方程的解．
答：该种干果的第一次进价是每千克5元；
（2）[
| 3000 |
| 5 |
| 9000 |
| 5×(1+20%) |
=（600+1500-600）×9+4320-12000
=1500×9+4320-12000
=13500+4320-12000
=5820（元）．
答：超市销售这种干果共盈利5820元．
点评：本题考查分式方程的应用，分析题意，找到合适的等量关系是解决问题的关键．
练习册系列答案
激活思维优加课堂系列答案
活力试卷系列答案
相关题目
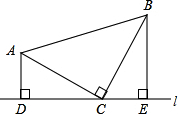已知：如图，等腰三角形ABC中，AC=BC，∠ACB=90°，直线l经过点C（点A、B都在直线l的同侧），AD⊥l，BE⊥l，垂足分别为D、E．
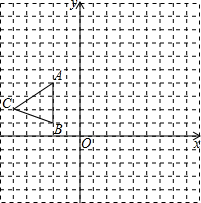如图，在平面直角坐标系xOy中，△ABC三个顶点坐标分别为A（-2，4），B（-2，1），C（-5，2）．
如图，在⊙O的内接△ABC中，∠ACB=90°，AC=2BC，过C作AB的垂线l交⊙O于另一点D，垂足为E．设P是