题目内容
 如图,已知正方形ABCD,把边DC绕D点顺时针旋转30°到DC′处,连接AC′,BC′,CC′,写出图中所有的等腰三角形,并写出推理过程.
如图,已知正方形ABCD,把边DC绕D点顺时针旋转30°到DC′处,连接AC′,BC′,CC′,写出图中所有的等腰三角形,并写出推理过程.考点:正方形的性质,全等三角形的判定与性质,等腰三角形的判定与性质,旋转的性质
专题:证明题,压轴题
分析:利用旋转的性质以及正方形的性质进而得出等腰三角形,再利用全等三角形的判定与性质判断得出.
解答: 解;图中的等腰三角形有:△DCC′,△DC′A,△C′AB,△C′BC,
解;图中的等腰三角形有:△DCC′,△DC′A,△C′AB,△C′BC,
理由:∵四边形ABCD是正方形,
∴AB=AD=DC,∠BAD=∠ADC=90°,
∴DC=DC′=DA,
∴△DCC′,△DC′A为等腰三角形,
∵∠C′DC=30°,∠ADC=90°,
∴∠ADC′=60°,
∴△AC′D为等边三角形,
∴AC′=AD=AB,
∴△C′AB为等腰三角形,
∵∠C′AB=90°-60°=30°,
∴∠CDC′=∠C′AB,
在△DCC′和△ABC′中
,
∴△DCC′≌△ABC′(SAS),
∴CC′=C′B,
∴△BCC′为等腰三角形.
 解;图中的等腰三角形有:△DCC′,△DC′A,△C′AB,△C′BC,
解;图中的等腰三角形有:△DCC′,△DC′A,△C′AB,△C′BC,理由:∵四边形ABCD是正方形,
∴AB=AD=DC,∠BAD=∠ADC=90°,
∴DC=DC′=DA,
∴△DCC′,△DC′A为等腰三角形,
∵∠C′DC=30°,∠ADC=90°,
∴∠ADC′=60°,
∴△AC′D为等边三角形,
∴AC′=AD=AB,
∴△C′AB为等腰三角形,
∵∠C′AB=90°-60°=30°,
∴∠CDC′=∠C′AB,
在△DCC′和△ABC′中
|
∴△DCC′≌△ABC′(SAS),
∴CC′=C′B,
∴△BCC′为等腰三角形.
点评:此题主要考查了等腰三角形的判定以及全等三角形的判定与性质等知识,得出△AC′D为等边三角形是解题关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
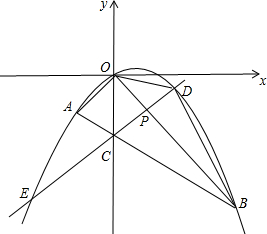 如图所示,在平面直角坐标系中,点A的坐标为(m,m),点B的坐标为(n,-n),抛物线经过A、O、B三点,连接OA、OB、AB,线段AB交y轴于点C.已知实数m、n(m<n)分别是方程x2-2x-3=0的两根.
如图所示,在平面直角坐标系中,点A的坐标为(m,m),点B的坐标为(n,-n),抛物线经过A、O、B三点,连接OA、OB、AB,线段AB交y轴于点C.已知实数m、n(m<n)分别是方程x2-2x-3=0的两根.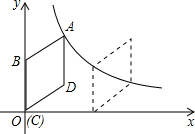 如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的
如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的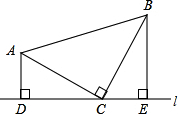 已知:如图,等腰三角形ABC中,AC=BC,∠ACB=90°,直线l经过点C(点A、B都在直线l的同侧),AD⊥l,BE⊥l,垂足分别为D、E.
已知:如图,等腰三角形ABC中,AC=BC,∠ACB=90°,直线l经过点C(点A、B都在直线l的同侧),AD⊥l,BE⊥l,垂足分别为D、E.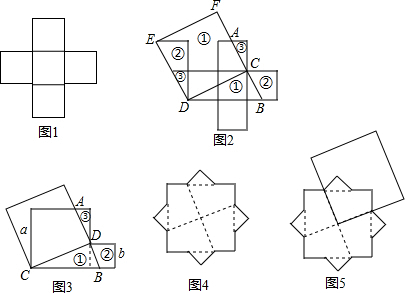
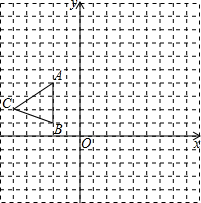 如图,在平面直角坐标系xOy中,△ABC三个顶点坐标分别为A(-2,4),B(-2,1),C(-5,2).
如图,在平面直角坐标系xOy中,△ABC三个顶点坐标分别为A(-2,4),B(-2,1),C(-5,2). 如图,在四边形ABCD中,AD=12,DO=OB=5,AC=26,∠ADB=90°.
如图,在四边形ABCD中,AD=12,DO=OB=5,AC=26,∠ADB=90°. 如图,平行于BC的直线DE把△ABC分成的两部分面积相等,则
如图,平行于BC的直线DE把△ABC分成的两部分面积相等,则