题目内容
14.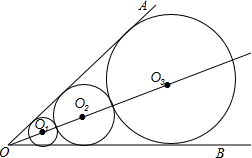 如图所示,已知∠AOB=60°,☉O1与∠AOB的两边都相切,沿OO1方向做☉O2与∠AOB的两边相切,且与☉O1外切,再作☉O3与∠AOB的两边相切,且与☉O2外切,…,如此作下去,☉On与∠AOB的两边相切,且与☉On-1外切,设☉On的半径为rn,已知r1=1则r2016=32015.
如图所示,已知∠AOB=60°,☉O1与∠AOB的两边都相切,沿OO1方向做☉O2与∠AOB的两边相切,且与☉O1外切,再作☉O3与∠AOB的两边相切,且与☉O2外切,…,如此作下去,☉On与∠AOB的两边相切,且与☉On-1外切,设☉On的半径为rn,已知r1=1则r2016=32015.
分析 作辅助线,构建直角三角形,根据相似三角形的性质分别求半径r2、r3、…、并找规律,得出结论.
解答 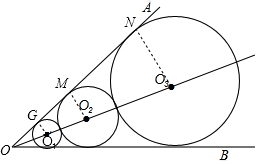 解:设⊙O1、⊙O2、⊙O3与边OA的切点为G、M、N,
解:设⊙O1、⊙O2、⊙O3与边OA的切点为G、M、N,
连接O1G、O2M、O3N,
则O1G⊥OA、O2M⊥OA、O3N⊥OA,
∴O1G∥O2M∥O3N,
∵⊙O1与∠AOB的两边都相切,∠AOB=60°,
∴∠AOO1=∠BOO1=30°,
∵OG=r1=1,
∴OO1=2,
∵O1G∥O2M,
∴△OO1G∽△OO2M,
∴$\frac{{O}_{1}G}{{O}_{2}M}$=$\frac{O{O}_{1}}{O{O}_{2}}$,
∴$\frac{1}{{r}_{2}}$=$\frac{2}{2+1+{r}_{2}}$,
∴r2=3,
同理得:$\frac{3}{{r}_{3}}$=$\frac{6}{6+3+{r}_{3}}$,
∴r3=9=32,
…
∴r2016=32015,
故答案为:32015.
点评 本题考查了切线长定理和切线的性质,本题可以看作是从圆外一点引圆的两条切线,可以得它们的切线长相等,圆心和这一点的连线,平分两条切线的夹角.根据这此结论与平行相似的判定结合,利用相似三角形的性质依次求圆的半径即可.

练习册系列答案
相关题目
9.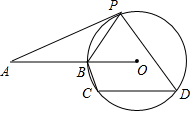 如图,AP为☉O的切线,P为切点,若∠A=20°,C、D为圆周上两点,且∠PDC=60°,则∠OBC等于( )
如图,AP为☉O的切线,P为切点,若∠A=20°,C、D为圆周上两点,且∠PDC=60°,则∠OBC等于( )
 如图,AP为☉O的切线,P为切点,若∠A=20°,C、D为圆周上两点,且∠PDC=60°,则∠OBC等于( )
如图,AP为☉O的切线,P为切点,若∠A=20°,C、D为圆周上两点,且∠PDC=60°,则∠OBC等于( )| A. | 55° | B. | 65° | C. | 70° | D. | 75° |
19.已知∠A=30°,下列判断正确的是( )
| A. | sinA=$\frac{1}{2}$ | B. | cosA=$\frac{1}{2}$ | C. | tanA=$\frac{1}{2}$ | D. | cotA=$\frac{1}{2}$ |
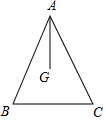 如图,G为△ABC的重心,如果AB=AC=13,BC=10,那么AG的长为8.
如图,G为△ABC的重心,如果AB=AC=13,BC=10,那么AG的长为8.