题目内容
11.某生物实验室需培育一群有益菌.现有60个活体样本,经过两轮培植后,总和达24000个,其中每个有益菌每一次可分裂出若干个相同数目的有益菌.每轮分裂中平均每个有益菌可分裂出19个有益菌?分析 设每轮分裂中平均每个有益菌可分裂出x个有益菌,则第一轮分裂后有(60+60x)个,第二轮分裂出(60+60x)x,两次加起来共有24000建立方程求出其解就可以.
解答 解:设每轮分裂中平均每个有益菌可分裂出x个有益菌,由题意,得
60(1+x)+60x(1+x)=24000,
60(1+x)(1+x)=24000,
解得:x1=19,x2=-21(舍去).
答:每轮分裂中平均每个有益菌可分裂出19个有益菌.
故答案为:19.
点评 本题考查了一元二次方程的实际运用,解答时分别表示出每轮分解后的总数得出数量关系是关键.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
2.若关于一元二次方程x2+2x+k+2=0的两个根相等,则k的取值范围是( )
| A. | 1 | B. | 1或-1 | C. | -1 | D. | 2 |
16.已知|a|=1,|b|=3,则|a+b|的值为( )
| A. | 2 | B. | 4 | C. | 2或4 | D. | ±2或±4. |
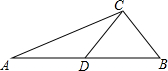 如图,在△ABC中,AB边上的中线CD=3,AB=6,BC+AC=8,
如图,在△ABC中,AB边上的中线CD=3,AB=6,BC+AC=8,