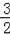题目内容
类比等腰三角形的定义,我们定义:有一组邻边相等的凸四边形叫做“等邻边四边形”.
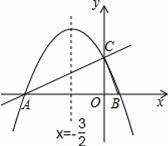
(1)如图1,在四边形ABCD中,添加一个条件使得四边形ABCD是“等邻边四边形”.请写出你添加的一个条件.
(2)小红猜想:对角线互相平分的“等邻边四边形”是菱形.她的猜想正确吗?请说明理由.
(3)如图2,小红作了一个Rt△ABC,其中∠ABC=90°,AB=2,BC=1,并将Rt△ABC沿∠ABC的平分线BB′方向平移得到△A′B′C′,连结AA′,BC′.小红要使得平移后的四边形ABC′A′是“等邻边四边形”,应平移多少距离(即线段B′B的长)?

【考点】四边形综合题.
【分析】(1)利用“等邻边四边形”的定义直接判断即可,
(2)利用平行四边形的判定和“等邻边四边形”的定义直接判断即可,
(3)利用“等邻边四边形”的定义和平移的性质(对应线段平行且相等),分四种情况(AA′=AB,AA′=A′C′,A′C′=BC′,BC′=AB)进行讨论计算即可.
【解答】(1)解:AB=BC或BC=CD或CD=AD或AD=AB
(2)解:小红的结论正确.
理由如下:∵四边形的对角线互相平分,
∴这个四边形是平行四边形,
∵四边形是“等邻边四边形”,
∴这个四边形有一组邻边相等,
∴这个“等邻边四边形”是菱形,
(3)解:由∠ABC=90°,AB=2,BC=1,得:AC=
 ,
,
∵将Rt△ABC平移得到Rt△A′B′C′,
∴BA′=AA′,A′B′∥AB,A′B′=AB=2,B′C′=BC=1,A′C′=AC=
 ,
,


(I)如图1,当AA′=AB时,BB′=AA′=AB=2,


(II)如图2,当AA′=A′C′时,BB′=AA′=AC′=
 ,
,


(III)当AC′=BC′=
 时,如图3,延长C′B′交AB于点D,则C′B′⊥AB
时,如图3,延长C′B′交AB于点D,则C′B′⊥AB
∵BB′平分∠ABC,
∴∠ABB′=
 ∠ABC=45°
∠ABC=45°
∴∠BB′D=∠ABB′=45°,
∴B′D=BD,
设B′D=BD=x,则C′D=x+1,BB′=
 x
x
∵根据在Rt△BC′D中,BC′2=C′D2+BD2即x2+(x+1)2=5
解得:x=1或x=﹣2(不合题意,舍去)
∴BB′=
 ,
,


(IV)当BC′=AB=2时,如图4,与(III)方法同理可得:x=
 或x=
或x=
 ,
,
x=
 或x=
或x=
 (舍去)
(舍去)
∴BB′=
 x=
x=
 .
.
故应平移2或
 或
或
 或
或
 .
.
【点评】本题是四边形的综合题,利用“等邻边四边形”的定义这个信息解决问题,涉及到了图形的平移的性质,得出BB′=AA′,A′B′∥AB,A′B′=AB=2,B′C′=BC=1,A′C′=AC,角的平分线的性质,由BB′平分∠ABC得到∠ABB′=
 ∠ABC=45°,勾股定理,解题的关键是理解“等邻边四边形”的定义的前提下,结合已学知识会用它.
∠ABC=45°,勾股定理,解题的关键是理解“等邻边四边形”的定义的前提下,结合已学知识会用它.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案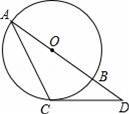


 OA
OA


 B.
B.



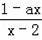
 +2=
+2=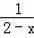
 有整数解的概率是 .
有整数解的概率是 .
 并将不等式组的解集在数轴上表示出来.
并将不等式组的解集在数轴上表示出来.


 x+2与x轴交于点A,与y轴交于点C.抛物线y=ax2+bx+c的对称轴是x=﹣
x+2与x轴交于点A,与y轴交于点C.抛物线y=ax2+bx+c的对称轴是x=﹣