题目内容
19.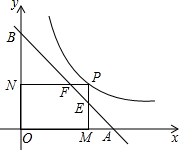 如图,P为反比例函数y=$\frac{3}{2x}$(x>0)图象上一点,过点P分别向x轴,y轴作垂线,垂足分别为M、N,直线y=-x+2与PM、PN分别交于点E、F,与x轴、y轴分别交于A、B,则AF•BE的值为3.
如图,P为反比例函数y=$\frac{3}{2x}$(x>0)图象上一点,过点P分别向x轴,y轴作垂线,垂足分别为M、N,直线y=-x+2与PM、PN分别交于点E、F,与x轴、y轴分别交于A、B,则AF•BE的值为3.
分析 由条件可知,△AOB是等腰直角三角形,故过F点作FH⊥x轴于H,则△AFH也是等腰直角三角形,故AH=FH,AF=$\sqrt{2}$FH=$\sqrt{2}$PM,过E点作EG⊥y轴于G点,则△BGE为等腰直角三角形,同理BE=$\sqrt{2}$PN,即可推出AF×BE=$\sqrt{2}$PM×$\sqrt{2}$PN=2PM•PN,由PM•PN=$\frac{3}{2}$,即可推出AF•BE的值.
解答  解:解:过F点作FH⊥x轴于H,过E点作EG⊥y轴于G,
解:解:过F点作FH⊥x轴于H,过E点作EG⊥y轴于G,
∵直线y=-x+2与x轴、y轴分别交于A、B,
∴A(2,0),B(0,2),
∴△AOB是等腰直角三角形,
∴△AFH也是等腰直角三角形,△BGE为等腰直角三角形,
∴AH=FH,BG=EG,
∴AF=$\sqrt{2}$FH=$\sqrt{2}$PM,BE=$\sqrt{2}$PN,
∴AF×BE=$\sqrt{2}$PM×$\sqrt{2}$PN=2PM•PN,
∵y=$\frac{3}{2x}$,
∴PM•PN=$\frac{3}{2}$,
∴AF×BE=2PM•PN=2×$\frac{3}{2}$=3.
故答案为3.
点评 本题主要考查反比例函数的性质、直线解析式的性质、等腰直角三角形的判定与性质,关键在于作出辅助线构建等腰直角三角形,由题意推出PM•PN=$\frac{1}{2}$和AF=$\sqrt{2}$PM、BE=$\sqrt{2}$PN.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
10.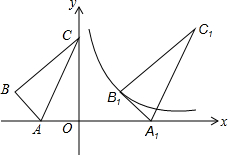 如图,△ABC的顶点A,C落在坐标轴上,且顶点B的坐标为(-5,2),将△ABC沿x轴向右平移得到△A1B1C1,使得点B1恰好落在函数y=$\frac{6}{x}$上,若线段AC扫过的面积为48,则点C1的坐标为( )
如图,△ABC的顶点A,C落在坐标轴上,且顶点B的坐标为(-5,2),将△ABC沿x轴向右平移得到△A1B1C1,使得点B1恰好落在函数y=$\frac{6}{x}$上,若线段AC扫过的面积为48,则点C1的坐标为( )
 如图,△ABC的顶点A,C落在坐标轴上,且顶点B的坐标为(-5,2),将△ABC沿x轴向右平移得到△A1B1C1,使得点B1恰好落在函数y=$\frac{6}{x}$上,若线段AC扫过的面积为48,则点C1的坐标为( )
如图,△ABC的顶点A,C落在坐标轴上,且顶点B的坐标为(-5,2),将△ABC沿x轴向右平移得到△A1B1C1,使得点B1恰好落在函数y=$\frac{6}{x}$上,若线段AC扫过的面积为48,则点C1的坐标为( )| A. | (3,2) | B. | (5,6) | C. | (8,6) | D. | (6,6) |
7.如果x-2y=5,xy=-2,那么(x+2y)2=( )
| A. | 17 | B. | 21 | C. | 23 | D. | 9 |
17. 如图,在△ABC中∠A=80°.点D是BC延长线上一点,∠ACD=150°,则∠B=( )
如图,在△ABC中∠A=80°.点D是BC延长线上一点,∠ACD=150°,则∠B=( )
 如图,在△ABC中∠A=80°.点D是BC延长线上一点,∠ACD=150°,则∠B=( )
如图,在△ABC中∠A=80°.点D是BC延长线上一点,∠ACD=150°,则∠B=( )| A. | 60° | B. | 50° | C. | 70° | D. | 165° |
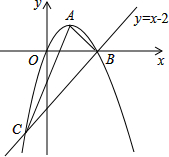 如图,已知抛物线经过原点O,顶点为A(1,1),且与直线y=x-2交于B,C两点.
如图,已知抛物线经过原点O,顶点为A(1,1),且与直线y=x-2交于B,C两点.