题目内容
5.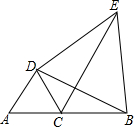 如图,点C在线段AB上,△DAC和△DBE都是等边三角形,试说明:△DAB≌△DCE.
如图,点C在线段AB上,△DAC和△DBE都是等边三角形,试说明:△DAB≌△DCE.
分析 由△DAC和△DBE都是等边三角形,利用等边三角形的性质得到两对边相等,两个角为60度,利用等式的性质得到夹角相等,利用SAS即可得证.
解答 证明:∵△DAC和△DBE都是等边三角形,
∴DA=DC,DB=DE,∠ADC=∠BDE=60°,
∴∠ADC+∠CDB=∠BDE+∠CDB,
即∠ADB=∠CDE,
在△DAB和△DCE中,$\left\{\begin{array}{l}{DA=DC}&{\;}\\{∠ADB=∠CDE}&{\;}\\{DB=DE}&{\;}\end{array}\right.$
∴△DAB≌△DCE(SAS).
点评 此题考查了全等三角形的判定与性质,以及等边三角形的性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
10.将一块木板钉在墙上,我们至少需要2个钉子将它固定,这是因为( )
| A. | 两点确定一条直线 | B. | 两点确定一条线段 | ||
| C. | 两点之间,直线最短 | D. | 两点之间,线段最短 |
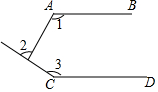 如图,已知AB∥CD,∠1=115°,∠3=140°,则∠2=75°.
如图,已知AB∥CD,∠1=115°,∠3=140°,则∠2=75°.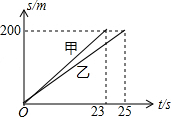 如图所示的是甲、乙两人在争夺冠军中的比赛图,其中t表示赛跑时所用时间,s表示赛跑的距离,根据图象回答下列问题:
如图所示的是甲、乙两人在争夺冠军中的比赛图,其中t表示赛跑时所用时间,s表示赛跑的距离,根据图象回答下列问题: