题目内容
4.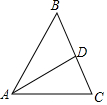 如图,在△ABC中,AD平分∠BAC.
如图,在△ABC中,AD平分∠BAC.(1)作线段AD的垂直平分线EF交AB边于点E,交AC边于点F;
(保留作图痕迹,不写作法)
(2)若BD=3,CD=2,AF=4,求BE的长.
分析 (1)根据中垂线的尺规作图可得;
(2)先利用中垂线的性质及全等三角形的性质证四边形AEDF是菱形,再证△BED∽△DFC得$\frac{BE}{DF}=\frac{BD}{CD}$,即可得出答案.
解答 解:(1)如图,直线EF即为所求;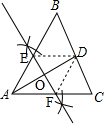
(2)由(1)知EF垂直平分AD,
∴EA=ED、FA=FD,∠AOE=∠AOF=90°,
∵AD平分∠BAC,
∴∠BAD=∠CAD,
在△AEO和△AFO中,
∵$\left\{\begin{array}{l}{∠EAO=∠FAO}\\{AO=AO}\\{∠AOE=∠AOF}\end{array}\right.$,
∴△AEO≌△AFO(ASA),
∴AE=AF,
则AE=DE=AF=DF,
∴四边形AEDF是菱形,
∴DE=DF=AF=4,DE∥AC、DF∥AB,
∴∠FDC=∠B,∠DFC=∠BAC=∠BED,
∴△BED∽△DFC,
∴$\frac{BE}{DF}=\frac{BD}{CD}$,即$\frac{BE}{4}$=$\frac{3}{2}$,
则BE=6.
点评 本题主要考查作图-基本作图,熟练掌握中垂线的性质、全等三角形的判定与性质及菱形的判定与性质、相似三角形的判定与性质是解题的关键.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
14.下列图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  等边三角形 | B. |  正方形 | C. |  平行四边形 | D. |  正五边形 |
12. 下列俯视图正确的是( )
下列俯视图正确的是( )
 下列俯视图正确的是( )
下列俯视图正确的是( )| A. |  | B. |  | C. |  | D. |  |
19.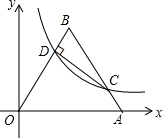 如图,将边长为2的等边△OAB放置于平面直角坐标系xOy中,C是AB边上的一个点(不与端点A、B重合),作CD⊥OB于点D,若点C、D都在双曲线y=$\frac{k}{x}$上(k>0,x>0),则k的值为( )
如图,将边长为2的等边△OAB放置于平面直角坐标系xOy中,C是AB边上的一个点(不与端点A、B重合),作CD⊥OB于点D,若点C、D都在双曲线y=$\frac{k}{x}$上(k>0,x>0),则k的值为( )
 如图,将边长为2的等边△OAB放置于平面直角坐标系xOy中,C是AB边上的一个点(不与端点A、B重合),作CD⊥OB于点D,若点C、D都在双曲线y=$\frac{k}{x}$上(k>0,x>0),则k的值为( )
如图,将边长为2的等边△OAB放置于平面直角坐标系xOy中,C是AB边上的一个点(不与端点A、B重合),作CD⊥OB于点D,若点C、D都在双曲线y=$\frac{k}{x}$上(k>0,x>0),则k的值为( )| A. | $\frac{9}{16}$$\sqrt{3}$ | B. | $\frac{3}{4}$$\sqrt{3}$ | C. | $\frac{9}{25}$$\sqrt{3}$ | D. | $\frac{3}{5}$$\sqrt{3}$ |
9.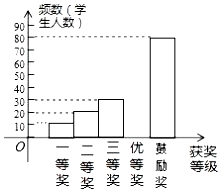 为了进一步普及足球知识,传播足球文化,某市举行了“足球进校园”知识竞赛活动,为了解足球知识的普及情况,随机抽取了部分获奖情况进行整理,得到下列不完整的统计图表:
为了进一步普及足球知识,传播足球文化,某市举行了“足球进校园”知识竞赛活动,为了解足球知识的普及情况,随机抽取了部分获奖情况进行整理,得到下列不完整的统计图表:
请根据所给信息,解答下列问题:
(1)a=60,b=0.15;
(2)补全频数分布直方图;
(3)在这次竞赛中,甲、乙、丙、丁四位同学都获得一等奖,若从这四位同学中随机选取两位同学代表该市参加上一级竞赛,请用树状图或列表的方法,计算恰好选中甲、乙二人的概率.
 为了进一步普及足球知识,传播足球文化,某市举行了“足球进校园”知识竞赛活动,为了解足球知识的普及情况,随机抽取了部分获奖情况进行整理,得到下列不完整的统计图表:
为了进一步普及足球知识,传播足球文化,某市举行了“足球进校园”知识竞赛活动,为了解足球知识的普及情况,随机抽取了部分获奖情况进行整理,得到下列不完整的统计图表:| 获奖等次 | 频数 | 频率 |
| 一等奖 | 10 | 0.05 |
| 二等奖 | 20 | 0.10 |
| 三等奖 | 30 | b |
| 优胜奖 | a | 0.30 |
| 鼓励奖 | 80 | 0.40 |
(1)a=60,b=0.15;
(2)补全频数分布直方图;
(3)在这次竞赛中,甲、乙、丙、丁四位同学都获得一等奖,若从这四位同学中随机选取两位同学代表该市参加上一级竞赛,请用树状图或列表的方法,计算恰好选中甲、乙二人的概率.
16.如图,是某几何体的三视图及相关数据,则该几何体的表面积是( )


| A. | 39π | B. | 29π | C. | 24π | D. | 19π |
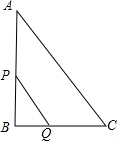 如图,在Rt△ABC中,∠B=90°,AC=10cm,BC=6cm,现有两点P,Q分别从点A和点C同时出发,沿边AB,CB向终点B移动.其中点P,Q的速度分别为2cm/s,1cm/s,且当其中一点到达终点时,另一点也随之停止移动.设P,Q两点移动时间为x s.
如图,在Rt△ABC中,∠B=90°,AC=10cm,BC=6cm,现有两点P,Q分别从点A和点C同时出发,沿边AB,CB向终点B移动.其中点P,Q的速度分别为2cm/s,1cm/s,且当其中一点到达终点时,另一点也随之停止移动.设P,Q两点移动时间为x s. 如图,已知一次函数y1=$\frac{4}{3}$x-4与反比例函数y2=$\frac{k}{x}$的图象在第一象限相交于点A(6,n),与x轴相交于点B.
如图,已知一次函数y1=$\frac{4}{3}$x-4与反比例函数y2=$\frac{k}{x}$的图象在第一象限相交于点A(6,n),与x轴相交于点B.