题目内容
11.类比特殊四边形的学习,我们可以定义:有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形”.探索体验
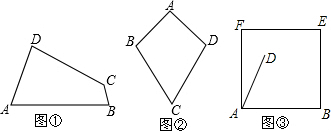
(1)如图①,已知四边形ABCD是“等对角的四边形”,∠A≠∠C,∠A=70°,∠B=80°,求∠C,∠D的度数.
(2)如图②,若AB=AD=a,CB=CD=b,且a<b,那么四边形ABCD是“等对角四边形”吗?试说明理由.
尝试应用
(3)如图③,在边长为5的正方形木板ABEF上裁出“等对角四边形”ABCD,若已经确定DA=4,∠DAB=60°.能否在正方形ABEF内(包括边上)确定点C,使四边形ABCD为面积最大的“等对角四边形”?若能确定出点C,试求四边形ABCD的最大面积;若不能确定,请说明理由.
分析 (1)由四边形ABCD是“等对角四边形”,∠A≠∠C,∠A=70°,∠B=80°,根据定义,即可求得∠D的度数,然后由四边形内角和定理,求得∠C的度数.
(2)首先连接BD,由AB=AD=a,CB=CD=b,且a≠b,可得∠ABD=∠ADC,△ABD与△CBD不相似,即∠A≠∠C,则可证得结论;
(3)首先连接BD,由当∠DAB=∠BCD=60°时,四边形ABCD是“等对角四边形”,可得此时点C在BD为弦的$\widehat{CD}$上,即可得要使四边形ABCD的面积最大,则点C在边BE上,然后过点D作DH⊥AB于点H,作DM⊥BC于点M,利用勾股定理求解即可求得答案.
解答  解:(1)∵四边形ABCD是“等对角四边形”,∠A≠∠C,∠A=70°,∠B=80°,
解:(1)∵四边形ABCD是“等对角四边形”,∠A≠∠C,∠A=70°,∠B=80°,
∴∠D=∠B=80°,
∴∠C=360°-80°-80°-70°=130°;
(2)证明:如图2,连接BD,
∵AB=AD,CB=CD,
∴∠ABD=∠ADB,∠CBD=∠CDB,
∴∠ABD+∠CBD=∠ADB+∠CDB,
∴∠ABC=∠ADC,
∵AB=AD=a,CB=CD=b,且a≠b,且BD=BD,
∴△ABD与△CBD不相似,
∴∠A≠∠C,
∴四边形ABCD是“等对角四边形”.
(3)如图3,连接BD,
当∠DAB=∠BCD=60°时,四边形ABCD是“等对角四边形”,
此时点C在BD为弦的$\widehat{CD}$上,
要使四边形ABCD的面积最大,则点C在边BE上,
过点D作DH⊥AB于点H,作DM⊥BC于点M,
在Rt△ADH中,∠DAH=60°,AD=4,
∴AH=2,DH=2$\sqrt{3}$,
∴BH=AB-AH=4,
∵四边形DHBM是矩形,
∴BM=DH=2$\sqrt{3}$,DM=BH=4,
在Rt△DMC中,∠DCM=60°,
∴CM=$\frac{\sqrt{3}}{3}$DM=$\frac{4\sqrt{3}}{3}$,
∴BC=BM+CM=2$\sqrt{3}$+$\frac{4\sqrt{3}}{3}$=$\frac{10\sqrt{3}}{3}$,
∴S四边形ABCD=S△ABD+S△BCD=$\frac{1}{2}$×6×2$\sqrt{3}$+$\frac{1}{2}$×$\frac{10\sqrt{3}}{3}$×4=$\frac{38}{3}\sqrt{3}$.
点评 此题属于四边形的综合题.考查了矩形的性质、等腰三角形的性质以及相似三角形的判定等知识.注意准确作出辅助线是解此题的关键.

 阅读快车系列答案
阅读快车系列答案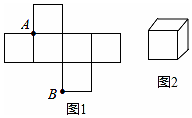 如图1是边长为1的六个小正方形组成的平面图形,将它围成图2的正方体,则图1中小正方形顶点A,B在围成的正方体上的距离是( )
如图1是边长为1的六个小正方形组成的平面图形,将它围成图2的正方体,则图1中小正方形顶点A,B在围成的正方体上的距离是( )| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | 1 | D. | 0 |
 a、b在数轴上的位置如图所示,那么化简|a-b|-$\sqrt{{a}^{2}}$的结果是( )
a、b在数轴上的位置如图所示,那么化简|a-b|-$\sqrt{{a}^{2}}$的结果是( )| A. | 2a-b | B. | b | C. | -b | D. | -2a+b |
| A. | 29个 | B. | 41个 | C. | 45个 | D. | 55个 |
| A. | 1.15×109 | B. | 11.5×107 | C. | 1.15×108 | D. | 1.158 |