题目内容
5.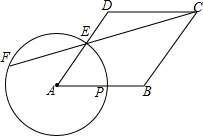 如图,边长为5的菱形ABCD中,cosA=$\frac{3}{5}$,点P为边AB上一点,以A为圆心,AP为半径的⊙A与边AD交于点E,射线CE与⊙A另一个交点为点F.
如图,边长为5的菱形ABCD中,cosA=$\frac{3}{5}$,点P为边AB上一点,以A为圆心,AP为半径的⊙A与边AD交于点E,射线CE与⊙A另一个交点为点F.(1)当点E与点D重合时,求EF的长;
(2)设AP=x,CE=y,求y关于x的函数关系式及定义域;
(3)是否存在一点P,使得$\widehat{EF}$=2$\widehat{PE}$?若存在,求AP的长;若不存在,请说明理由.
分析 (1)由平行四边形的性质得到∠AEF=DAB,再利用cos∠DAB=cos∠AEF=$\frac{EH}{AE}$=$\frac{3}{5}$即可求解;
(2)由平行四边形的性质得到∠CGD=∠BAD,再利用勾股定理即可求解;
(3)由平行四边形的性质得到∠GCE=∠HAE=∠DAB,利用cosA=$\frac{3}{5}$计算即可.
解答 解:(1)过点A作AH⊥EF于点H,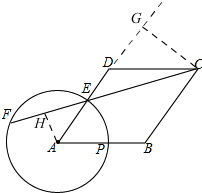 ∴EF=2EH,
∴EF=2EH,
∵点E与点D重合,
∴EF∥AB,
∴∠AEF=DAB,
∴cos∠DAB=cos∠AEF=$\frac{EH}{AE}$=$\frac{3}{5}$,
∵AE=5,
∴EH=3,
∴EF=6;
(2)如图,
过点C作CG⊥AD,
在Rt△CGD中,cos∠CDG=cos∠BAD=$\frac{3}{5}$,
∴DG=3,CG=4,
在Rt△CGE中,GE=8-x,
∴y2=16+(8-x)2,
y=$\sqrt{{x}^{2}-16x+80}$(0<x≤5),
(3)∵cos∠DAB=$\frac{3}{5}$,
∴tan∠DAB=$\frac{4}{3}$,
∵∠GCE=∠HAE=∠DAB,
∴tan∠DAB=$\frac{8-x}{4}$=$\frac{4}{3}$,
∴x=$\frac{8}{3}$,
即:AP的长为$\frac{8}{3}$.
点评 此题是圆的综合题,主要考查了圆的性质,平行四边形的性质,勾股定理以及锐角三角函数,锐角三角函数的运用是解本题的关键.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案
相关题目
16.如果60m表示“向北走60m”,那么“向南走20m”可以表示为( )
| A. | -20m | B. | -40m | C. | 20m | D. | 40m |
13.等腰三角形的一个角是90°,则它的底角是( )
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
 如图,在?ABCD中,O为BD的中点,过O作两条互相垂直的直线,分别交四边形ABCD于E,F,G,H,求证:四边形EFGH是菱形.
如图,在?ABCD中,O为BD的中点,过O作两条互相垂直的直线,分别交四边形ABCD于E,F,G,H,求证:四边形EFGH是菱形.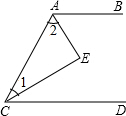 如图,AE平分∠BAC,CE平分∠ACD,且∠1+∠2=90°.试说明CD∥AB.
如图,AE平分∠BAC,CE平分∠ACD,且∠1+∠2=90°.试说明CD∥AB.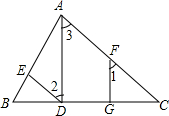 已知AD⊥BC,FG⊥BC,垂足分别为D、G,且∠1=∠2,求证∠BDE=∠C.
已知AD⊥BC,FG⊥BC,垂足分别为D、G,且∠1=∠2,求证∠BDE=∠C.