Question

1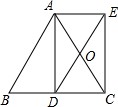．如图，AD是等腰△ABC底边BC上的高．点O是AC中点，延长DO到E，使OE=OD，连接AE，CE．
（1）求证：四边形ADCE的是矩形；
（2）若AB=17，BC=16，求四边形ADCE的面积．

Answer 1

分析 （1）根据平行四边形的性质得出四边形ADCE是平行四边形，根据垂直推出∠ADC=90°，根据矩形的判定得出即可；
（2）求出DC，根据勾股定理求出AD，根据矩形的面积公式求出即可．

解答 （1）证明：∵点O是AC中点，
∴AO=OC，
∵OE=OD，
∴四边形ADCE是平行四边形，
∵AD是等腰△ABC底边BC上的高，
∴∠ADC=90°，
∴四边形ADCE是矩形；

（2）解：∵AD是等腰△ABC底边BC上的高，BC=16，AB=17，
∴BD=CD=8，AB=AC=17，∠ADC=90°，
由勾股定理得：AD=$\sqrt{A{C}^{2}-C{D}^{2}}$=$\sqrt{1{7}^{2}-{8}^{2}}$=15，
∴四边形ADCE的面积是AD×DC=15×8=120．

点评 本题考查了平行四边形的判定，矩形的判定和性质，等腰三角形的性质，勾股定理的应用，能综合运用定理进行推理和计算是解此题的关键，比较典型，难度适中．