题目内容
7. 如图,菱形ABCD中,点M,N在AC上,ME⊥AD于点E,NF⊥AB于点F.若ME=3,NM=NF=2,则AN 的长为4.
如图,菱形ABCD中,点M,N在AC上,ME⊥AD于点E,NF⊥AB于点F.若ME=3,NM=NF=2,则AN 的长为4.
分析 根据菱形的对角线平分一组对角可得∠1=∠2,然后求出△AFN和△AEM相似,再利用相似三角形对应边成比例列出求解即可.
解答 解:在菱形ABCD中,∠1=∠2,
又∵ME⊥AD,NF⊥AB,
∴∠AEM=∠AFN=90°,
∴△AFN∽△AEM,
∴$\frac{AN}{AM}$=$\frac{NF}{ME}$,
即$\frac{AN}{AN+2}$=$\frac{2}{3}$,
解得AN=4.
故答案为:4.
点评 本题考查了菱形的对角线平分一组对角的性质,相似三角形的判定与性质,关键在于得到△AFN和△AEM相似.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
18.下列交通标志中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
2.如图1,在三角形纸片ABC中,∠A=78°,AB=4,AC=6.将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形相似的有( )


| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
12.已知点C在线段AB上,且点C是线段AB的黄金分割点(AC>BC),则下列结论正确的是( )
| A. | AB2=AC•BC | B. | BC2=AC•BC | C. | AC=$\frac{\sqrt{5}-1}{2}$BC | D. | BC=$\frac{3-\sqrt{5}}{2}$AB |
19.下列式子正确的是( )
| A. | -2.1>-2.01 | B. | -2>0 | C. | $\frac{1}{3}$<$\frac{1}{4}$ | D. | -15<13 |
16.已知关于x的方程x2+(2m-3)x+m2=0有两个实数根x1,x2,且x1+x2=x1•x2,则m=( )
| A. | m=-3或1 | B. | m=1 | C. | m=-3 | D. | m=-3且m≠0 |
17. 如图,钟面上的时间是8:30,再经过t分钟,时针、分针第一次重合,则t为( )
如图,钟面上的时间是8:30,再经过t分钟,时针、分针第一次重合,则t为( )
 如图,钟面上的时间是8:30,再经过t分钟,时针、分针第一次重合,则t为( )
如图,钟面上的时间是8:30,再经过t分钟,时针、分针第一次重合,则t为( )| A. | $\frac{75}{6}$ | B. | $\frac{150}{11}$ | C. | $\frac{150}{13}$ | D. | $\frac{180}{11}$ |
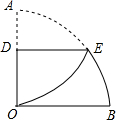 在扇形纸片AOB中,∠AOB=90°,OA=4,将扇形纸片AOB按如图所示折叠,使对折后点A与点O重合,折痕为DE,则$\widehat{BE}$的长度为$\frac{2}{3}$π.
在扇形纸片AOB中,∠AOB=90°,OA=4,将扇形纸片AOB按如图所示折叠,使对折后点A与点O重合,折痕为DE,则$\widehat{BE}$的长度为$\frac{2}{3}$π.