题目内容
18.若关于x的一元二次方程x2-x+k+1=0有两个不相等的实数根,则k的取值范围是k<-$\frac{3}{4}$.分析 根据判别式的意义得到△=(-1)2-4(k+1)>0,然后解不等式即可.
解答 解:根据题意得△=(-1)2-4(k+1)>0,
解得k<-$\frac{3}{4}$.
故答案为k<-$\frac{3}{4}$.
点评 本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:当△>0时,方程有两个不相等的实数根;当△=0时,方程有两个相等的实数根;当△<0时,方程无实数根.

练习册系列答案
相关题目
13. 如图,在矩形纸片ABCD中,AB=3,点E在边BC上,将△ABE沿直线AE折叠,点B恰好落在对角线AC上的点F处,若∠EAC=∠ECA,则AC的长是( )
如图,在矩形纸片ABCD中,AB=3,点E在边BC上,将△ABE沿直线AE折叠,点B恰好落在对角线AC上的点F处,若∠EAC=∠ECA,则AC的长是( )
 如图,在矩形纸片ABCD中,AB=3,点E在边BC上,将△ABE沿直线AE折叠,点B恰好落在对角线AC上的点F处,若∠EAC=∠ECA,则AC的长是( )
如图,在矩形纸片ABCD中,AB=3,点E在边BC上,将△ABE沿直线AE折叠,点B恰好落在对角线AC上的点F处,若∠EAC=∠ECA,则AC的长是( )| A. | $3\sqrt{3}$ | B. | 6 | C. | 4 | D. | 5 |
7.经过圆锥顶点的截面的形状可能是( )
| A. |  | B. |  | C. |  | D. |  |
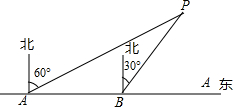 为了维护国家主权和海洋权利,海监部门对我国领海实现了常态化巡航管理,如图,正在执行巡航任务的海监船以每小时50海里的速度向正东方航行,在A处测得灯塔P在北偏东60°方向上,继续航行1小时到达B处,此时测得灯塔P在北偏东30°方向上.
为了维护国家主权和海洋权利,海监部门对我国领海实现了常态化巡航管理,如图,正在执行巡航任务的海监船以每小时50海里的速度向正东方航行,在A处测得灯塔P在北偏东60°方向上,继续航行1小时到达B处,此时测得灯塔P在北偏东30°方向上.


 如图,AB与CD相交于点E,AC∥DB,△ACE与△BDE是位似图形吗?
如图,AB与CD相交于点E,AC∥DB,△ACE与△BDE是位似图形吗?