题目内容
4.一个不透明的袋中装有红、黄、白三种颜色球共50个,它们除颜色外都相同,其中黄球个数是白球个数的3倍少5个,已知从袋中摸出一个球是红球的概率是$\frac{3}{10}$.(1)求袋中红球的个数;
(2)求从袋中摸出一个球是白球的概率;
(3)取走5个球(其中没有红球)后,求从剩余的球中摸出一个球是红球的概率.
分析 (1)根据红、黄、白三种颜色球共有的个数乘以红球的概率即可;
(2)设白球有x个,得出黄球有(3x+10)个,根据题意列出方程,求出白球的个数,再除以总的球数即可;
(3)先求出取走5个球后,还剩的球数,再根据红球的个数,除以还剩的球数即可.
解答 解:(1)根据题意得:
50×$\frac{3}{10}$=15(个),
答:袋中红球的个数有15个.
(2)设白球有x个,则黄球有(3x-5)个,
根据题意得x+3x-5=50-15
解得x=10.
则摸出一个球是白球的概率P=$\frac{10}{50}$=$\frac{1}{5}$;
(3)因为取走5个球后,还剩45个球,其中红球的个数没有变化,
所以从剩余的球中摸出一个球是红球的概率是$\frac{15}{45}$=$\frac{1}{3}$.
点评 此题考查了概率公式:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=$\frac{m}{n}$.

练习册系列答案
相关题目
15.小明做投掷骰子(质地均匀的正方体)实验,共做了100次实验,实验的结果如下:
(1)计算“4点朝上”的频率.
(2)小明说:“根据实验,一次实验中出现3点朝上的概率最大”.他的说法正确吗?为什么?
(3)小明投掷一枚骰子,计算投掷点数小于3的概率.
| 朝上的点数 | 1 | 2 | 3 | 4 | 5 | 6 |
| 出现的次数 | 14 | 15 | 23 | 16 | 20 | 12 |
(2)小明说:“根据实验,一次实验中出现3点朝上的概率最大”.他的说法正确吗?为什么?
(3)小明投掷一枚骰子,计算投掷点数小于3的概率.
16.将抛物线y=x2向右平移2个单位,再向下平移1个单位,得到的抛物线是( )
| A. | y=(x-2)2-1 | B. | y=(x-2)2+1 | C. | y=(X+2)2+1 | D. | y=(x+2)2-1 |
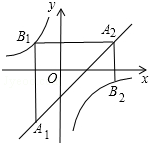 如图,已知点A1,A2,…,An均在直线y=x-1上,点B1,B2,…,Bn均在反比例函数y=-$\frac{1}{x}$的图象上,并且满足:A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,…,AnBn⊥x轴,BnAn+1⊥y轴,…,记点An的横坐标为an(n为正整数).若a1=-1,则a2017=-1.
如图,已知点A1,A2,…,An均在直线y=x-1上,点B1,B2,…,Bn均在反比例函数y=-$\frac{1}{x}$的图象上,并且满足:A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,…,AnBn⊥x轴,BnAn+1⊥y轴,…,记点An的横坐标为an(n为正整数).若a1=-1,则a2017=-1.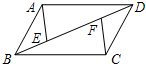 如图,在?ABCD中,E,F是对角线BD上的两点且BE=DF,联结AE,CF.
如图,在?ABCD中,E,F是对角线BD上的两点且BE=DF,联结AE,CF.