题目内容
13.已知x,y,z为三个非负实数,满足$\left\{\begin{array}{l}{x+y+z=30}\\{2x+3y+4z=100}\end{array}\right.$,若s=3x+2y+5z,则s的最小值为90.分析 把$\left\{\begin{array}{l}{x+y+z=30}\\{2x+3y+4z=100}\end{array}\right.$看作为关于x和y的二元一次方程组,然后利用加减消元法可得到x=z-10,y=-2z+40,把x=z-10,y=-2z+40代入s=3x+2y+5z中得S=4z+50,再根据x,y,z为三个非负实数,即z-10≥0,-2z+40≥0,z≥0,解得10≤z≤20,然后根据一次函数的性质求解.
解答 解:$\left\{\begin{array}{l}{x+y+z=30①}\\{2x+3y+4z=100②}\end{array}\right.$,
①×3-②得3x-2x+3z-4z=-10,
解得x=z-10,
①×2-②得2y-3y+2z-4z=-40,
解得y=-2z+40;
∵x=z-10,y=-2z+40;
∴S=3(z-10)+2(-2z+40)+5z
=4z+50,
∵x,y,z为三个非负实数,
∴z-10≥0,-2z+40≥0,z≥0,
∴10≤z≤20,
当z=10时,S有最小值,最小值=40+50=90.
故答案为90.
点评 本题考查了三元一次方程组:利用加减消元法或代入消元法把三元一次方程组转化为二元一次方程组求解.也考查了一次函数的性质.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
3.下列计算正确的是( )
| A. | a3•a3=2a6 | B. | a3+a3=a6 | C. | ${a^3}÷{a^5}=\frac{1}{a^2}$ | D. | (a3)3=a6 |
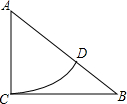 如图,在Rt△ABC中,∠ACB=90°,以点A为圆心,AC长为半径作圆弧交边AB于点D.若 AC=3,BC=4.则BD的长是( )
如图,在Rt△ABC中,∠ACB=90°,以点A为圆心,AC长为半径作圆弧交边AB于点D.若 AC=3,BC=4.则BD的长是( )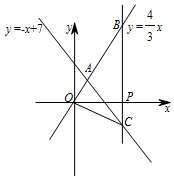 如图:在平面直角坐标系xOy中,已知正比例函数$y=\frac{4}{3}x$与一次函数y=-x+7的图象交于点A.
如图:在平面直角坐标系xOy中,已知正比例函数$y=\frac{4}{3}x$与一次函数y=-x+7的图象交于点A.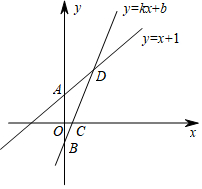 如图,已知直线y=x+1与y轴交于点A,一次函数y=kx+b的图象经过点B(0,-1),与x轴以及y=x+1的图象分别交于点C、D,且点D的坐标为(1,n).
如图,已知直线y=x+1与y轴交于点A,一次函数y=kx+b的图象经过点B(0,-1),与x轴以及y=x+1的图象分别交于点C、D,且点D的坐标为(1,n).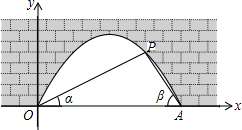 图中是抛物线拱桥,P处有一照明灯,水面OA宽4m,从O、A两处观测P处,仰角分别为α、β,且tanα=$\frac{1}{2}$,tanβ=$\frac{3}{2}$,以O为原点,OA所在直线为x轴建立直角坐标系.
图中是抛物线拱桥,P处有一照明灯,水面OA宽4m,从O、A两处观测P处,仰角分别为α、β,且tanα=$\frac{1}{2}$,tanβ=$\frac{3}{2}$,以O为原点,OA所在直线为x轴建立直角坐标系.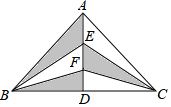 如图,在Rt△ABC中,∠BAC=90°,AB=AC=4,点E、F是高AD上的三等分点,则图中阴影部分的面积是( )
如图,在Rt△ABC中,∠BAC=90°,AB=AC=4,点E、F是高AD上的三等分点,则图中阴影部分的面积是( )