题目内容
12.先化简,再请你用喜爱的数代入求值:$\frac{{m}^{2}-2m+1}{{m}^{2}-1}$÷(1-$\frac{1}{m+1}$).分析 先化简题目中的式子,然后选取一个使得原分式有意义的m的值代入即可解答本题,注意m不等于0,-1,1.
解答 解:$\frac{{m}^{2}-2m+1}{{m}^{2}-1}$÷(1-$\frac{1}{m+1}$)
=$\frac{(m-1)^{2}}{(m+1)(m-1)}÷\frac{m+1-1}{m+1}$
=$\frac{m-1}{m+1}×\frac{m+1}{m}$
=$\frac{m-1}{m}$,
当m=2时,原式=$\frac{2-1}{2}=\frac{1}{2}$.
点评 本题考查分式的化简求值,解答本题的关键是明确分式化简求值的方法.

练习册系列答案
相关题目
2.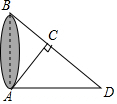 如图所示,为了测量出A、B两点间的距离,在地面上找到一点C,连接AC、BC,使得∠ACB=90°,然后在BC的延长线上确定点D,使得CD=CB.现已知AD的长是一元一次方程$\frac{x-7}{2}$+$\frac{x+4}{7}$=26的解,则A、B两点间的距离为( )
如图所示,为了测量出A、B两点间的距离,在地面上找到一点C,连接AC、BC,使得∠ACB=90°,然后在BC的延长线上确定点D,使得CD=CB.现已知AD的长是一元一次方程$\frac{x-7}{2}$+$\frac{x+4}{7}$=26的解,则A、B两点间的距离为( )
 如图所示,为了测量出A、B两点间的距离,在地面上找到一点C,连接AC、BC,使得∠ACB=90°,然后在BC的延长线上确定点D,使得CD=CB.现已知AD的长是一元一次方程$\frac{x-7}{2}$+$\frac{x+4}{7}$=26的解,则A、B两点间的距离为( )
如图所示,为了测量出A、B两点间的距离,在地面上找到一点C,连接AC、BC,使得∠ACB=90°,然后在BC的延长线上确定点D,使得CD=CB.现已知AD的长是一元一次方程$\frac{x-7}{2}$+$\frac{x+4}{7}$=26的解,则A、B两点间的距离为( )| A. | 30米 | B. | 35米 | C. | 40米 | D. | 45米 |
20.-|-2017|的相反数是( )
| A. | 2017 | B. | $\frac{1}{2017}$ | C. | -2017 | D. | -$\frac{1}{2017}$ |
7.计算$\sqrt{2}$sin30°+tan60°-cos45°的结果是( )
| A. | $\sqrt{2}$ | B. | $\sqrt{2}$-$\frac{1}{2}$ | C. | $\sqrt{3}$ | D. | $\frac{\sqrt{3}}{3}$ |
17.下列二次根式中,与$\sqrt{2}$之积为有理数的是( )
| A. | $\sqrt{18}$ | B. | $\sqrt{\frac{3}{4}}$ | C. | $\sqrt{12}$ | D. | -$\sqrt{27}$ |
4.数轴上点A、B表示的数分别是a,b,则点A,B之间的距离为( )
| A. | a+b | B. | a-b | C. | |a+b| | D. | |a-b| |
1. 在?ABCD中,E为AD的中点,则△DEF与△BCF的面积比为( )
在?ABCD中,E为AD的中点,则△DEF与△BCF的面积比为( )
 在?ABCD中,E为AD的中点,则△DEF与△BCF的面积比为( )
在?ABCD中,E为AD的中点,则△DEF与△BCF的面积比为( )| A. | 1:2 | B. | 1:3 | C. | 1:4 | D. | 1:$\sqrt{2}$ |