题目内容
3.在一个不透明的盒子中装有3个形状大小完全一样的小球,上面分别有标号1,2,-1,用树状图或列表的方法解决下列问题:(1)将球搅匀,从盒中一次取出两个球,求其两标号互为相反数的概率.
(2)将球搅匀,摸出一个球将其标号记为k,放回后搅匀后再摸出一个球,将其标号记为b.求直线y=kx+b不经过第三象限的概率.
分析 (1)列表得到所有可能的结果即可求出两标号互为相反数的概率;
(2)列表得到所有可能的结果,要注意是不放回事件,即可求出一次函数y=kx+b的图象不经过第三象限的概率.
解答 解:(1)列表得:
| (2,1) | (-1,1) | |
| (1,2) | (-1,2) | |
| (1,-1) | (2,-1) |
所以两标号互为相反数的概率=$\frac{2}{6}$=$\frac{1}{3}$;
(2)列表如下:
| 1 | -1 | 2 | |
| 1 | y=x+1 | y=x-1 | y=x+2 |
| -1 | y=-x+1 | y=-x-1 | y=-x+2 |
| 2 | y=2x+1 | y=2x-1 | y=2x+2 |
点评 此题考查的是用列表法或树状图法求概率.注意树状图法与列表法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;注意概率=所求情况数与总情况数之比.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
14.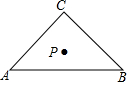 如图,已知在Rt△ABC中,∠C=90°,AC=BC,AB=6,点P是Rt△ABC的重心,则点P到AB所在直线的距离等于( )
如图,已知在Rt△ABC中,∠C=90°,AC=BC,AB=6,点P是Rt△ABC的重心,则点P到AB所在直线的距离等于( )
 如图,已知在Rt△ABC中,∠C=90°,AC=BC,AB=6,点P是Rt△ABC的重心,则点P到AB所在直线的距离等于( )
如图,已知在Rt△ABC中,∠C=90°,AC=BC,AB=6,点P是Rt△ABC的重心,则点P到AB所在直线的距离等于( )| A. | 1 | B. | $\sqrt{2}$ | C. | $\frac{3}{2}$ | D. | 2 |
8.下列运算正确的是( )
| A. | (a2)3=a5 | B. | (ab)2=ab2 | C. | a6÷a3=a2 | D. | a2•a3=a5 |
12.若点A(m,n)在一次函数y=3x+b的图象上,且3m-n>2,则b的取值范围为( )
| A. | b>2 | B. | b>-2 | C. | b<2 | D. | b<-2 |
14.若$\left\{\begin{array}{l}{x=a}\\{y=b}\end{array}\right.$(a≠0)是方程2x+y=0的一个解,则( )
| A. | a和b同号 | B. | a和b异号 | ||
| C. | a和b可能同号也可能异号 | D. | a≠0,b=0 |
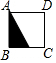
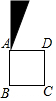
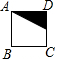 如图,将正方形ABCD中的阴影三角形绕点A顺时针旋转90°后,得到的图形为( )
如图,将正方形ABCD中的阴影三角形绕点A顺时针旋转90°后,得到的图形为( )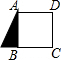
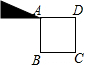
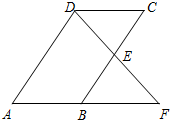 已知,如图,平行四边形ABCD中,E是BC边的中点,连DE并延长交AB的延长线于点F,求证:AB=BF.
已知,如图,平行四边形ABCD中,E是BC边的中点,连DE并延长交AB的延长线于点F,求证:AB=BF.