题目内容
18.(1)完成下列推理,并填写理由已知:DE⊥AO于E,BO⊥AO,∠CFB=∠EDO,证明:CF∥DO
证明:∵DE⊥AO,BO⊥AO(已知)
∴∠DEA=∠BOA=90°(垂直的定义 )
∵DE∥BO(同位角相等,两直线平行 )
∴∠EDO=∠DOB(两直线平行,内错角相等 )
又∵∠CFB=∠EDO(已知 )
∴∠DOF=∠CFB(等量代换 )
∴CF∥DO(同位角相等,两直线平行 )
(2)如图,已知:AD∥BC,AD=CB,AE=CF,请问∠B=∠D吗?为什么?

分析 (1)根据垂直的定义得到∠DEA=∠BOA,根据平行线的判定得到DE∥BO,利用平行线的性质得到∠EDO=∠DOB,等量代换得到∠DOF=∠CFB,根据平行线的判定得到结论;
(2)首先由平行线的性质得∠A=∠C,由AE=CF可得AF=CE,利用全等三角形的判定定理和性质定理可得结论.
解答 (1)证明:∵DE⊥AO,BO⊥AO(已知)
∴∠DEA=∠BOA=90°(垂直的定义)
∵DE∥BO(同位角相等,两直线平行)
∴∠EDO=∠DOB(两直线平行,内错角相等)
又∵∠CFB=∠EDO(已知)
∴∠DOF=∠CFB(等量代换)
∴CF∥DO(同位角相等,两直线平行);
故答案为:垂直的定义;同位角相等,两直线平行;∠DOB;两直线平行,内错角相等;已知;等量代换;同位角相等,两直线平行
(2)解:∠B=∠D.
∵AD∥BC,
∴∠A=∠C,
∵AE=CF,
∴AE+EF=CF+EF,
∴AF=CE,
在△ADF与△CBE中,
$\left\{\begin{array}{l}{AD=CB}\\{∠A=∠C}\\{AF=CE}\end{array}\right.$,
∴△ADF≌△CBE(SAS),
∴∠B=∠D.
点评 本题考查了平行线的性质和判定以及全等三角形的性质和判定定理,熟练掌握平行线的性质是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.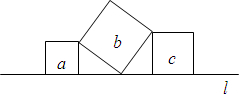 如图,直线l上有三个正方形a、b、c,若a、c的边长分别为1和2,则b的面积为( )
如图,直线l上有三个正方形a、b、c,若a、c的边长分别为1和2,则b的面积为( )
 如图,直线l上有三个正方形a、b、c,若a、c的边长分别为1和2,则b的面积为( )
如图,直线l上有三个正方形a、b、c,若a、c的边长分别为1和2,则b的面积为( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
9. 如图,梯子AB靠在墙上,梯子的底端A到墙根O的距离为2m,梯子的顶端B到地面的距离为7m,现将梯子的底端A向外移动到A′,使梯子的底端A′到墙根O的距离等于3m,同时梯子的顶端B下降至B′,那么BB′( )
如图,梯子AB靠在墙上,梯子的底端A到墙根O的距离为2m,梯子的顶端B到地面的距离为7m,现将梯子的底端A向外移动到A′,使梯子的底端A′到墙根O的距离等于3m,同时梯子的顶端B下降至B′,那么BB′( )
 如图,梯子AB靠在墙上,梯子的底端A到墙根O的距离为2m,梯子的顶端B到地面的距离为7m,现将梯子的底端A向外移动到A′,使梯子的底端A′到墙根O的距离等于3m,同时梯子的顶端B下降至B′,那么BB′( )
如图,梯子AB靠在墙上,梯子的底端A到墙根O的距离为2m,梯子的顶端B到地面的距离为7m,现将梯子的底端A向外移动到A′,使梯子的底端A′到墙根O的距离等于3m,同时梯子的顶端B下降至B′,那么BB′( )| A. | 小于1m | B. | 大于1m | C. | 等于1m | D. | 小于或等于1m |
6.不等式5-x>2的解集是( )
| A. | x>-3 | B. | x>3 | C. | x<-7 | D. | x<3 |
13.平移边长为1的小菱形◇可以得到美丽的“中国结”图案,下面四个图案是由◇平移后得到的类似“中国结”的图案,其中第(1)个图形含边长为1的菱形2个,第(2)个图形含边长为1的菱形8个,第(3)个图形含边长为1的菱形18个,则第(8)个图形中含边长为1的菱形的个数是( )


| A. | 88 | B. | 98 | C. | 112 | D. | 128 |
3.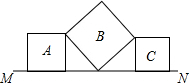 如图,在直线MN上有三个正方形A、B、C,若正方形A和正方形C的面积分别为16和20,则正方形B的面积为( )
如图,在直线MN上有三个正方形A、B、C,若正方形A和正方形C的面积分别为16和20,则正方形B的面积为( )
 如图,在直线MN上有三个正方形A、B、C,若正方形A和正方形C的面积分别为16和20,则正方形B的面积为( )
如图,在直线MN上有三个正方形A、B、C,若正方形A和正方形C的面积分别为16和20,则正方形B的面积为( )| A. | 24 | B. | 36 | C. | 40 | D. | 48 |
 如图,在平面直角坐标系xOy中,A(-3,0),B(0,1),形状相同的抛物线Cn(n=1,2,3,4,…)的顶点在直线AB上,其对称轴与x轴的交点的横坐标依次为2,3,5,8,12,…,根据上述规律,抛物线Cn的顶点坐标为($\frac{{n}^{2}-n+4}{2}$,$\frac{{n}^{2}-n+10}{6}$).
如图,在平面直角坐标系xOy中,A(-3,0),B(0,1),形状相同的抛物线Cn(n=1,2,3,4,…)的顶点在直线AB上,其对称轴与x轴的交点的横坐标依次为2,3,5,8,12,…,根据上述规律,抛物线Cn的顶点坐标为($\frac{{n}^{2}-n+4}{2}$,$\frac{{n}^{2}-n+10}{6}$).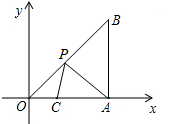 如图,在平面直角坐标系中,Rt△OAB的顶点A在x轴的正半轴上,顶点B的坐标为(4,4),点C的坐标为(1,0),点P为斜边OB上的一个动点,当PA+PC的值最小值时,点P的坐标为($\frac{4}{5}$,$\frac{4}{5}$).
如图,在平面直角坐标系中,Rt△OAB的顶点A在x轴的正半轴上,顶点B的坐标为(4,4),点C的坐标为(1,0),点P为斜边OB上的一个动点,当PA+PC的值最小值时,点P的坐标为($\frac{4}{5}$,$\frac{4}{5}$).